|
Constructing Functions from a TABLE: |
|
Constructing equations for exponential functions from a table of values may be a very simple process, or it may be a more challenging process, depending upon the information provided in the table.
Before we start, we should check to see if the table CAN BE represented by an exponential function. Remember that exponential functions grow by common factors over equal intervals.
Are the x-values changing by the same increment, and do successive y-values have a common factor? (The term "multiplier" will be used to represent "common factor".)
|
The table at the right shows values from an exponential function of the form
f (x) = abx.
Find the values of a and b, and express an equation that may be represented by this table.
This example would be labeled EASY since the
y-intercept is given at (0,7) and the ordered pairs
increase by the same x increment of 1. |
|
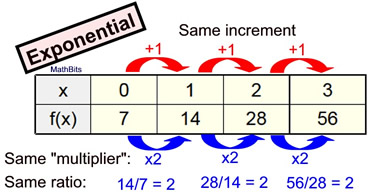
The ordered pair (0,7) is the y-intercept, so a = 7.
The "multiplier" is 2, so b = 2. |
| Solution:
In the last lesson, we saw that the y-intercept of f (x) = abx is (0, a).
So, in this example, we can see that the y-intercept is at (0,7) making a = 7. ANS: a = 7
Since we have already noted that the common factor ("multiplier") is 2 in this table, we know the value for b is 2. ANS: b = 2
Equation: f (x) = 7•(2)x |
What happens when the x-increment is NOT +1 ?
There is a detail about the "b" value in an exponential equation, f (x) = abx,
that we need to recognize when working with tables.
 Important Detail:
The multiplier, b, in an exponential equation is the constant factor by which the dependent variable changes for every unit increase in the independent variable.
This means that the multiplier, b, represents the ratio of consecutive y values when the x values increase by a unit of 1. |
The table at the right shows values from an exponential function.
Find the values of a and b, and express an equation that may be represented by this table.
Notice that the "same increment" is now +5 (instead of +1). This will affect the final answer, making this problem's difficulty level HARD. |
|
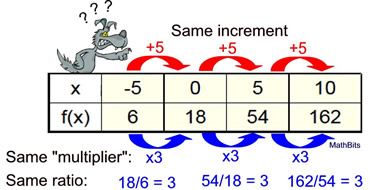
The y-intercept is (0,18), so a = 18.
But the "multiplier" of 3 is for every increment of 5.
So, now what happens? |
This is what happens when we proceed as we did in Example 1:
We are looking for our answer to be of the form f (x) = abx.
Again, we know that the y -intercept of f (x) = abx is (0, a). So, in this example, we can see that the y-intercept is at (0,18) making a = 18. ANS: a = 18
We will assume (incorrectly) that the common factor (or "multiplier") is 3 in this table, so the b value is 3.
ANS: b = 3
Equation: f (x) = 18•(3)x |
 |
This is not the correct equation!
f (5) = 18•(3)5 = 4374 ≠ 54 Nope! |
|
|
So, what went wrong?
The problem is that our formula, f (x) = abx, assumes that the increment on x will be +1.
So, the formula would see +5 to be the fifth increment to the right of zero, and not the first increment to the right of zero. The common factor is then applied 5 times, instead of only once, and we get an answer of 4374 instead of 54. |
 |
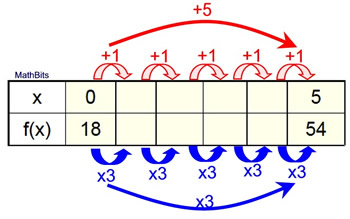How can we "fix" this problem?
The "multiplier" in this problem is being applied for an x-increment of 5 units (not 1 unit).
We need to make an adjustment that will reflect the needed change in the size of the x increment. That change will be to allow x to become x/5. |
| Equation: f (x) = 18•(3)x/5 |
| An adjustment to the formula: |
 |
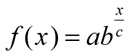where c = the
x-increment value |
|
|
|
Let's see how the graphing calculator can solve Example 2 above,
with an x-increment equal to +5.
Choose your calculator to see the Calculator's solution to Example 2.
What do we do when no consistent x-increment is given ?
The table at the right shows values from an exponential function of the form f (x) = abx.
Find the values of a and b, and express an equation that may be represented by this table.
This example would be labeled MODERATE difficulty, |
|
Notice: No constant increment on x.
No constant multiplier on f (x).
Now, what do we do?
x |
-1 |
1 |
4 |
6 |
9 |
f(x) |
0.75 |
3 |
24 |
96 |
768 |
We DO KNOW that this is an exponential function as the question says it's an exponential function. |
Solution:
We need a new plan of attack on this problem since it is not immediately obvious what the common factor ("multiplier") may be. Choose 2 of the points that are closest to one another, such as x = -1 and x = 1, or x = 4 and x = 6. If the decimal bothers you, choose x = 4 and
x = 6. Create a new section of the table filling in the missing increments between the two points you chose. |
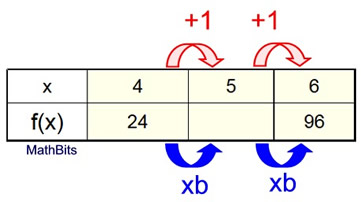"xb" means "times b" |
You can see that we represented the "multiplier" between each of the increments with "xb" to represent "times b". Now, algebraically, to get from f (x) = 24 to f (x) = 96 we have:
24 • b • b = 96 → 24b2 = 96 → b2 = 4 → b = 2
We now have: f (x) = a • 2x
To get a, substitute one of the points, such as (4,24).
24 = a • 24 = a • 16 → a = 24/16 = 1.5 |
Equation: f (x) = 1.5•(2)x |
Constructing Functions from TWO Input-Output PAIRS: |
|
|
"Do two points always determine an exponential function?"
Assuming that we are speaking about an exponential function of the form f (x) = abx,
the answer is "Yes, under certain conditions." The conditions are that:
[1] a ≠ 0 (because you would have a straight line),
[2] that the x-coordinates not be the same (you wouldn't have a function) and
[3] that the y-coordinates of the points be non-zero with the same signs (remember the asymptotic nature of the graphs of these exponential functions - always all above, or all below, the x-axis).
So, how do we change two points into an exponential function?
Constructing functions given only two input-output pairs (or ordered pairs) can be accomplished in a variety of ways. The choice of solution method will depend upon the nature of the given pairs. For example, if you are given the y-intercept as one pair, the solution will be fast and easy. If, on the other hand, you are given two generic pairs, perhaps containing decimals, you will need to do more work to find the solution. Let's take a look at some of the possibilities.
|
| Example 1: (easy) Find an exponential function of the form f(x) = abx given the facts that f(0) = 12 and f(5) = 2916. |
Solution:
f (0) = 12 → (0,12)
f (5) = 2916 → (5, 2916) |
Find a: The y-intercept is 12, so a = 12.
We now have f (x) = 12•bx |
Find b: Substitute:
2916 = 12•b5
243 = b5
b = 3 |
| Equation: f (x) = 12•(3)x (you can Check this answer by plugging in the two points.) |
| Example 2: (moderate) Given the graph shown at the right, find an exponential function to represent this graph. |
 |
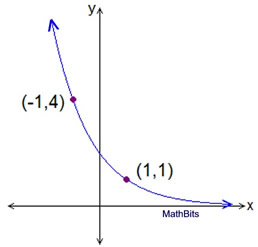Solution: Points (-1,4) and (1,1).
Since neither of these points is the y-intercept, and the y-intercept cannot be read from the graph, a system of equations will be needed to solve this problem.
f (x) = abx (remember b > 0 and b≠1)
The substitution method shown below is ONE method of solution. |
Substitute the points into the formula:
(-1,4) → f (-1) = ab-1 = 4
(1,1) → f (1) = ab1 = 1
|
Solve first equation for a:
 |
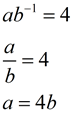Plug a into second equation :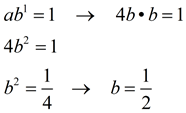
|
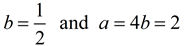
Equation: f (x) = 2•(½)x (you can Check this answer by plugging in the two points.) |
| Example 3: (harder) Find an exponential function of the form f(x) = abx which will pass through the points (1,30) and (3,187.5). |
| This problem will also require a system of equations. But, this time, we will be using an elimination method to solve, instead of the substitution method shown in Example 2. |
Solution:
Substitute the points into the formula:
(1, 30) → f (1) = ab1 = 30
(3,187.5) → f (3) = ab3 = 187.5 |
Divide the two equations:
This will be easier if you start with the larger exponent on top.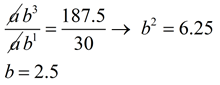
|
Plug in to find a:
 |
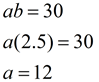| Equation: f (x) = 12•(2.5)x (you can Check this answer by plugging in the two points.) |
Let's see how the graphing calculator can solve Example 4 above,
given only two points.
Choose your calculator to see the Calculator's solution to Example 4.
NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|
