Using Graphing Calculator TI-84+ CE |
|
|
Let's see what the graphing calculator can do to solve "Example 2"
from the Algebra 2 lesson,
"Constructing Exponential Functions".
The algebraic solution for 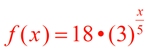this question gave the equation
 AGAIN:
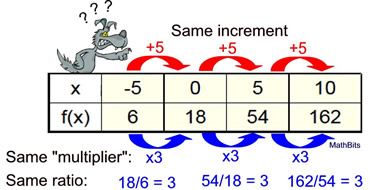
The table at the right shows values from an exponential function.
Find the values of a and b, and express an equation that may be represented by this table.
With use of the graphing calculator, the difficulty level will be lowered to MODERATE. |
|
 |
Solution: We will be using the graphing calculator's ability to prepare an exponential regression equation to find the solution to this problem. Under these conditions, we will be obtaining the actual equation (and not an approximation, or best fit, for the equation).
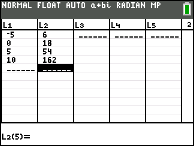
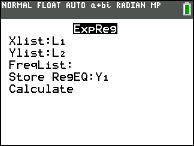
Enter the four points into
L1 and L2 under STAT
 |
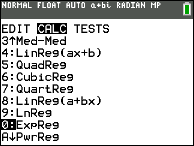
From STAT → CALC
choose 0:ExpReg
 |
Use the lists where you stored the points. Fill in Y1 for the graph.
 |
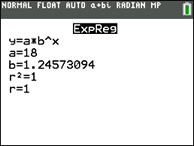 Note r2 = 1 and r = 1 are telling us we hit ALL of the points for an actual equation. |
a = 18 and b = 1.24573094
Equation: f (x) = 18•(1.24573094)x
But this doesn't match the algebraic answer, or does it?
Put those exponent skills to use!
It does match!
|
|
Let's see what the graphing calculator can do to solve "Example 4"
from the Algebra 2 lesson, "Constructing Exponential Functions".
The algebraic solution for this question gave the equation
f (x) = 4•(0.25)x
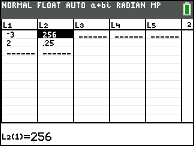
Example 4 AGAIN: (calculator) Find an exponential function of the form f(x) = abx which will pass through the points (-3,256) and (2, ¼). Round to nearest hundredths if needed.
We will solve this again, using the exponential regression capabilities of the graphing calculator. |
Solution:
Enter the two points into L1 and L2 under STAT
 |
From STAT → CALC choose 0:ExpReg
|
Be sure your lists match where you stored the points. Fill in Y1 if you want to see the graph.
|
|
a = 4
b = .25
Equation: f (x) = 4•(0.25)x
Aren't calculators wonderful!!
|
Return to the Algebra 2 lesson on Constructing Exponential Functions in Algebra 2.
