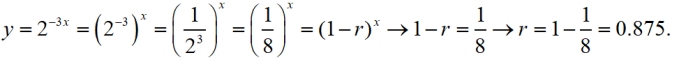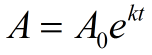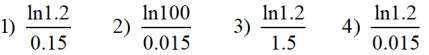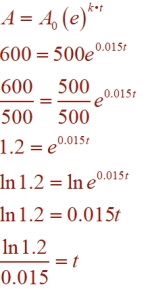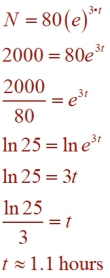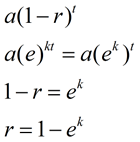|
Exponential growth and decay were introduced in Algebra 1.
In Algebra 2, we will review and expand these concepts.
The following two exponential formulas can be used to illustrate the concepts of exponential growth and decay in applied situations. If a quantity grows (or decays) by a fixed percentage at regular time intervals, the pattern can be depicted by these functions.
The function y = abx represents "discrete" growth (or decay).
For "growth", base b equals 1 + r. For "decay", base b equals 1 - r.
r is a "fixed percentage rate per time interval".
|
As it pertains to mathematics, "discrete" refers to dealing with distinct objects (such as fixed time intervals),
rather than continuous quantities (such as at every instant in time)
Exponential Growth:
y = a(1 + r)x
The growth factor is greater than 1. |
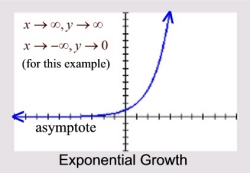
a > 0, (1 + r) > 1
|
Exponential Decay:
y = a(1 - r)x
The decay factor is less than 1. |
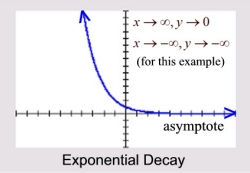
a > 0, 0 < (1 - r) < 1
|
Remember that the original exponential formula was y = abx.
You will notice that in these growth and decay functions,
base b, the growth factor, has been replaced by (1 + r) or by (1 - r).
This formula represents growth where the value is multiplied by a fixed base, b,
every time interval x. The growth rate, r, is constant, derived from b = 1 + r.
The growth "rate" ( r) is determined from b = 1 + r, giving r = b - 1.
The decay "rate" ( r) is determined from b = 1 - r, giving r = 1 - b
"r" is the fixed percent rate of growth or decay per time interval.
The percentage rate of growth represents a "step", " jump", or "chunk" of time.
a = initial value (the amount before measuring growth or decay)
r = growth or decay rate (most often represented as a percentage and expressed as a decimal)
x = number of time intervals that have passed
|
How to determine the percent rate of growth given y = abx:
For Growth: Given y = 32x, determine the percent rate of growth.
This function is equivalent to y = 9x, which is an increasing function (b > 1)
so we are looking at growth.
This example is in y = abx form, when we need it to be in y =
a(1 + r)x form to find r.
We need to write b as (1 + r) .
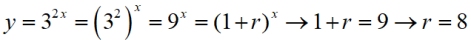
As a fixed percentage, r = 8.00 = 800% = percent rate of growth per interval
----------------------------------------------------
For Decay: Given y = 2-3x, determine the percent rate of decay.
This function is equivalent to y = (1/8)x, which is a decreasing function (0 < b < 1)
so we are looking at decay.
We need this equation to be in y =
a(1 - r)x form to find r.
We need to write b as (1 - r) .
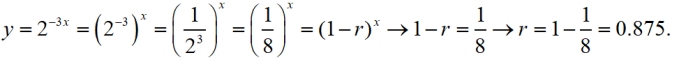
As a percentage, r = .875 = 87.5% = percent rate of decay per interval.
NOTE: This percent rate of change is "decay". It may be listed as -87.5% to "indicate" decay. This does not mean to substitute
-.875 as r into (1 - r), which already deals with the negative aspect of decay.
It simply means that the percent rate of decay is "associated" with a function that is decreasing. |
In the model, y = abx, base b is the growth factor.
If y = 3(1.15)x, then the percentage growth rate per time interval (such as weekly),
is r = 0.15 or 15% per week.
The y-value changes by a fixed percentage at each time interval (such as each week).

Remember that exponential growth describes a quantity that is increasing by a fixed percentage at regular (fixed) time intervals.
 The population of Home Town is 2026 was estimated to be 35,000 people with an annual rate of increase of 2.4%. The population of Home Town is 2026 was estimated to be 35,000 people with an annual rate of increase of 2.4%.
a) What is the growth factor for Home Town?
The "growth factor" refers to b as represented by (1 + r),
Since this problem deals with "increase", b = (1 + r) where r = 2.4% = 0.024
The growth factor 1 + r = 1 + 0.024 = 1.024. (Remember that growth factor is greater than 1.)
b) Write an equation to model future growth.
y = abx = a(1 + r)x = a(1.024)x = 35000(1.024)x
c) Use the equation to estimate the population in 2030 to the nearest hundred people.
There are 4 annual "time intervals" from 2026 to 2030, so x = 4.
y = 35000(1.024)4 ≈ 38,482.91 ≈ 38,500 |
|

Remember that exponential decay describes a quantity that is decreasing by a fixed percentage at regular (fixed) time intervals.
 The number of dolphin sitings in Baseline Cove, when first recorded, were 250 per year, but have been decreasing by 3% per year since that first siting. The number of dolphin sitings in Baseline Cove, when first recorded, were 250 per year, but have been decreasing by 3% per year since that first siting.
a) What is the decay factor for Baseline Cove sitings?
The "decay factor" refers to b as represented by (1 - r),
Since this problem deals with "decrease", b = (1 - r) where 3% = 0.03
The decay factor 1 - r = 1 - 0.03 = 0.97. (Remember that decay factor is between 0 and 1.)
b) Write an equation to model future decay.
y = abx = a(1 - r)x = a(0.97)x = 250(0.97)x
c) Use the equation to estimate the population of dolphins sited 5 years after the first siting. Round to nearest whole dolphin.
There are 5 annual "time intervals" for sitings in a 5 year period (x = 5).
y = 250(0.97)5 ≈ 214.6835064 ≈ 214 dolphins |
|

| Continuous Growth or Decay: |
The function y = aekx represents "continual" (or "natural") growth (or decay).
This function grows at every instant, meaning the "rate of growth"
equals the current value,
and not a fixed percentage.
A "fixed percentage rate per time interval" was seen with "discrete" growth for y = abx.. |
Most naturally occurring phenomena grow continuously. For example, bacteria will continue to grow over a 24 hour period, producing new bacteria which will also grow. The bacteria do not wait until the end of the 24 hours, and then all reproduce at once.
The exponential e is used when modeling continuous growth that occurs naturally such as populations, bacteria, radioactive decay, etc.
You can think of e like a universal constant representing how fast you could possibly grow using a continuous process.
And, the beauty of e is that not only is it used to represent "continuous growth", but it can also represent "discrete growth" measured periodically across time (such as the growth in Example 1).
In Algebra 2, the exponential e will be used in situations of continuous growth or decay.
The following formula is used to illustrate this continuous growth and decay model.
Continuous Exponential Growth or Decay
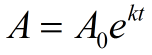
A = ending value (amount after growth or decay)
A0 = initial value (starting amount before measuring growth or decay)
e = exponential e = 2.71828183...
k = continuous growth rate (also called constant of proportionality)
(k > 0, the amount is increasing (growing); k < 0, the amount is decreasing (decaying))
t = time that has passed |
In this model the growth factor for one unit of time is ek.
The rate of growth (or decay) is equal to the current value of y.
This function is always growing (or decaying) at a rate proportional to its current size
described as 100% of its current size, instantaneously.
FYI: Is it possible to find a "fixed percentage rate of growth"
for y = aekt ?
Yes, but it is a bit confusing.
• The fixed % rate of growth is simply k • 100%, called the relative growth rate associated with continuous growth.
• To find the fixed % rate of growth, r, (seen in the discrete method) requires a conversion formula r = ek - 1, to determine the effective growth rate.
If we start with k = 5% (continuous growth rate)
1. evaluate function at t = 0 ( f (0) = 0) and t = 1 (f (1) = 1.0512)
2. evaluate % increase over 1 time unit, (f (1) - f (0)) / f(0) = 1.0512 - 1 = 0.0512
3. change to % so r = 5.12% (over one unit of time) |

 A chemical sample with an initial mass of 30 grams is decaying at a continuous rate of 7.2% per year. How many grams, to the nearest tenth, will remain after 4 years? A chemical sample with an initial mass of 30 grams is decaying at a continuous rate of 7.2% per year. How many grams, to the nearest tenth, will remain after 4 years?
 |
The rate of continuous decay will be a negative value
(k < 0). So, k = -7.2%. Fortunately, we have sufficient information to fill in the entire right side of the equation. This will make the solution a simple computation of the right side. |
 The current enrollment in the nursing program at a local community college is 500 students. The enrollment is increasing continuously at a rate of 1.5% each year. Which logarithm is equal to the number of years it will take for the enrollment to increase to 600? The current enrollment in the nursing program at a local community college is 500 students. The enrollment is increasing continuously at a rate of 1.5% each year. Which logarithm is equal to the number of years it will take for the enrollment to increase to 600?
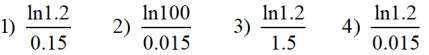
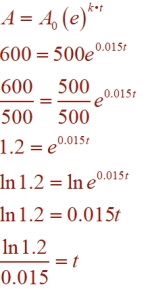 |
Substitute into the equation:
A0 = 500
A = 600
k = 0.015
To solve for t, we need to isolate the e0.015t.
Take ln of both sides, using the inverse relationship on the right.
Choice 4.
FYI: This is approximately 12.2years.
|
 The number of bacteria in a Petri dish is continuously increasing. This situation is modeled by the exponential function N = 80e3t, with N = the number of bacteria present in the Petri dish after t hours. Find, to the nearest hundredth, the number of hours it will take to reach 2000 bacteria. The number of bacteria in a Petri dish is continuously increasing. This situation is modeled by the exponential function N = 80e3t, with N = the number of bacteria present in the Petri dish after t hours. Find, to the nearest hundredth, the number of hours it will take to reach 2000 bacteria.
N = N0 ekt
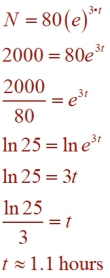 |
You may see the general formula written with different letters.
Since the value of k is positive 3, this is continuous growth.
Substitute 2000 for N (the desired end result) and solve for t.
Use the natural log (ln) to solve for t, since it is the inverse operation used when working with e.
Round answer to nearest hundredth.
|

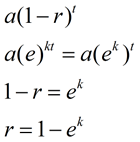
ek = 1 - r |
Comparing the two models:
On the left (looking at decay):
If we compare a(1 - r)t with aekt,
with our knowledge of rewriting exponents,
we can see how ek is related to
the rate of decay, r.
(Same process can be applied for growth.) |
FYI:
y = abt
y = ae (lnb) t
where k = lnb
is continuous rate |
The work on the left, shows that the continuous decay facor ek, over one unit of time,
is identical to the discrete decay multiplier (1 - r),
showing that the two methods of describing decay are mathematically equivalent
over one unit of time.

To see more about continuous growth and decay,
go to Doubling and Half-Life and Financial Interest.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|