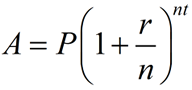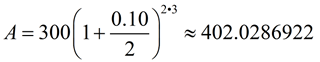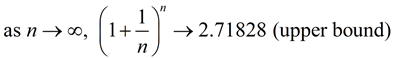|
As we look at financial interest, we will be looking at rates of growth.
No one wants their money to "decay".
The amount of interest earned by investing your money may be calculated in a variety of ways.
We are going to take a look at calculating:
(1) simple interest rates
(2) compounded interest rates (ammual and other time periods)
(3) continuously compounded interest rates |

|
I = P x R x T and A = P(1 + rt) |
You were finding simple interest when you used the formula I = P x R x T.
(Interest = Principal x Rate x Time)
When working with simple interest, your
total accrued amount (A),
or principal + interest, will be:
A = P + I = P + Prt = P(1 + rt).
Example: Karla invests $300 at a simple annual interest rate of 10% for 3 years. At the end of three years, Karla will have earned $90 in interest. I = P x R x T = 300 x 0.10 x 3 = $90.
With simple interest, Karla is earning $30 a year on this investment. The interest is ALWAYS based upon the original amount, not on her new yearly totals. She will continue to get the same $30 interest for each year, and the interest will be paid out at the end of each year.
End of Year 1: $300 + 0.1(300) = $330
End of Year 2: $330 + 0.1(300) = $360
End of Year 3: $360 + 0.1(300) = $390 |
At the end of the 3 years. Karla will have
A = 300(1 + 0.10(3)) = 300(1.3) =
$390 in her account. |

|
A = P(1 + r)t |
Look familiar?
y = a(1 + r)x |
By using compound interest, your interest earns interest.
ALL of the money you have at the end of each year will be used to calculate your new interest earned.
|
A = accrued amount
P = Principal (starting amount)
r = interest rate
t = time in years |
|
Example: Karla invests $300 compounded annually at a rate of 10% for 3 years. At the end of three years, Karla will have earned $99.30 in interest and have $399.30 in her account.
With compound interest, the interest Karla earns each year is used to compute the new interest for the next year.
End of Year 1: $300 + 0.1(300) = $330
End of Year 2: $330 + 0.1(330) = $363
End of Year 3: $363 + 0.1(363) = $399.30 |
At the end of the three years, Karla will have
A = 300(1 + 0.10)3 = 300(1.10)3 =
$399.30 in her account. |

|
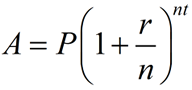 |
A = accrued
P = Principal
r = interest rate
n = number of
times per year compounded
t = time in years
|
We just saw that compound interest will get us more money. But won't we get even MORE money if we compound it more often - say every 6 months, instead of once a year?
Yes, compounding more often will increase the interest earned.
.
Note: Compounding more often applies a lower interest rate more often
which results in more money.
So, this new formula will allow for multiple time periods, n,
per year, t, for the compounding to occur.
Notice in this formula that you are:
(1) dividing the rate, r, by the number of compoundings per year, n, to get the rate per each new compounding period of time, r/n, and then
(2)
raising that new growth factor, (1 + r/n) to the number of compounding periods, nt, over the entire number of years, t. |
|
The value of n when compounding:
• annual (yearly) = 1
• semi-annual = 2
• quarterly = 4
• monthly = 12
• daily = 365 |
As n grows larger, we will get more interest. |
Example: Karla invests $300 compounded every 6 months at a rate of 10% for 3 years. At the end of three years, Karla will have $402.03 in her account.
As with the last compound interest, this interest which Karla earns every 6 months is used to compute the new interest. The annual rate of 10% will be divided by 2, creating the new 6-month rate of 5%. But because this lower rate of 5% will be applied twice as often, it will yield a slight increase in the total interest acquired over the three years.
|
At the end of the three years, Karla will have
$402.03 in her account. |

Continuous Compounding Interest
|
|
|
Look familiar?
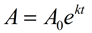 |
If decreasing the time periods between the compounding will increase the interest earned, then the best option is to have the interest compounded continuously (every second, every nanosecond, instantaneously). We want n (n = number of
times per year compounded) to approach infinity. Then every instant, the interest is hypothetically computed and added to the balance. While this is not actually possible, continuous compounding is defined as "the upper bound of compound interest".
As you compound more often, the effective annual rate increases. But it will not increase indefinitely. It will tend to a finite value which is an upper bound that is approached as the frequency of compounding increases. When the effective annual rate is at this upper bound, it is said that the interest is being compounded continuously.
When the interest of an annual rate of 1 is compounded n time a year, we have
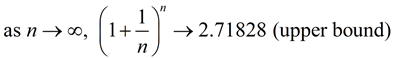
which is the exponential e ( which = 2.71828...).
Example: Karla invests $300 continuously compounded at a rate of 10% for 3 years. At the end of three years, Karla will have $404.96 in her account.
|
At the end of the three years, Karla will have
$404.96 in her account. |