|
Exponential doubling and half-life are specific measures of exponential growth and decay.
The result of these calculations is usually the time required for a specific change to occur.
"Doubling" is most often seen in relation to population, nature, or finance,
while "half-life" is prevalent in science, especially radioactive decay.

Let's get a visual picture of what "doubling" looks like and establish an equation.
EXAMPLE: A population of beetles in a Memorial Garden doubles every 3 months.
The population initially started with 18 beetles. How many beetles are in
the garden after 12 months (assuming all of the beetles survive)? |
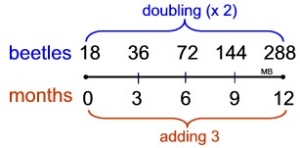
The diagram shows there are
4 "time intervals" at work
in this problem, and
that at the
end of 12 months there will be
288 beetles in the garden. |
Let's apply our findings from the last unit.
y = abx = a(1 + r)x for a growth model.
The growth, under doubling, is 100% growth.
So, the equation becomes y = a(1 + 1)x = a(2)x
where x = number of "time intervals" that have passed.
But, what do we use for x? We know that the number of beetles double every 3 months, but we need to know how many times this doubling occurred in the time period of 12 months to get the "time intervals". That will be 12 / 3.
So, the number of "time intervals" is the total time elapsed, t, divided by the time needed to double, d.
(t / d = 12/ 3 = 4 time intervals - Yep!)
Our growth model for doubling
is now y = a(2)t / d
where t = total time elapsed,
and d = time needed to double.
| x = t / d = "time intervals" that have passed related to "doubling" time, d. |
ANSWER: y = 18(2)4 = 288 beetles |

There are two ways to address the measures of "doubling" and "half-life".
One method uses the values of "2" and "½" for the base values,
while the other method uses "e" as the base value.
REMEMBER: We established that e is not only used to represesnt "continuous growth",
but can also represent "discrete growth" measured periodically over time.
D O U B L I N G
Base 2 will use the model we developed in our search for x (at the top of this page).
Doubling:
A = A0 • 2 t / d
A = end result
A0 = starting value
t = total time elapsed
d = time needed to double
|
With this formula, the doubling will occur at the end of "intervals" of time passed.
Example:
• A culture of bacteria, containing initially 60 bacteria, doubles every 30 minutes. Find the number of bacteria after 8 hours.
Establish the formula:
A0 = 60 A = 120 (double)
t = 30 min.

when needed.
|
Base e is used in populations, science, and finance as it describes continuous growth.
Doubling:
A = A0 • e kt
A = end result
A0 = initial value
t = total time elapsed
k = continuous growth rate |
Continuous growth occurs "all of the time",
not in "intervals" (or chunks) of time.
Example:
• A culture of bacteria, containing initially 60 bacteria, doubles every 30 minutes. Find the number of bacteria after 8 hours.
Establish the formula:
A0 = 60 A = 120 (double)
t = 30 min.
With this method, we need to first find k
so we can establish the equation needed.
 IMPORTANT: Keep the exact value (or the full 10-digit calculator display) throughout the solution. Round only the final answer, if needed. IMPORTANT: Keep the exact value (or the full 10-digit calculator display) throughout the solution. Round only the final answer, if needed. |
Notice the equation 2 = 1 • ek(30) in the solution above on the right.
Since we know "doubling" will occur, we can fast forward to this equation
using "2" for A and "1" for A0 whenever we have a doubling question
The "end result" is always "twice the starting value",
so the equation entries will always reduce down to "2" and "1", respectively.
 (discrete growth: Solve using A = A0 • 2 t / d ) (discrete growth: Solve using A = A0 • 2 t / d )
A strain of bacteria growing on your desktop doubles every 5 minutes. Assuming that you start with only "one" bacterium, how many bacteria could be present at the end of 96 minutes?
A0 = 1, t = 96, d = 5 minutes.
A = A0 • 2 t / d
A = 1 • 2 96/5
A = 602248.7631
A = 602248 bacteria
|
All of the time measurements are in minutes, so no time conversions were needed.
Simply substitute into the formula and solve.
Remember to round to the nearest living bacterium (no fractions of a bacterium). |
|
 (bacteria continuous growth: A = A0ekt ) (bacteria continuous growth: A = A0ekt )
A strain of bacteria growing on your desktop doubles every 5 minutes. Assuming that you start with only "one" bacterium, how many bacteria could be present at the end of 96 minutes?
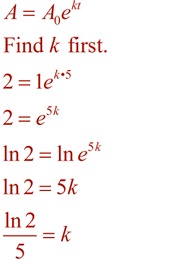
Finding k gives you the needed information to establish a formula specific for this strain of bacteria. |
The fact that you are "doubling" the amount within each 5 minute time period means that with an initial value (say "x"), you will always get "2x" at the end of the time.
You can establish a general formula that states:
2x = x • ekt for doubling, which simplifies to 2 = 1 • ekt.
You can see this simplified formula at work in the computations on the left, to solve for k. Using this solution, establish a specific equation for this bacteria. Solve for the "end result", A, using time (t) to be 96 minutes. Round to nearest whole bacterium.
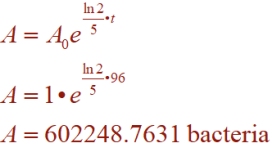
Answer: 602248 bacteria
|
|
|
|

H A L F - L I F E
Half-life is a term generally associated with chemical reactants and radioisotopes.
It is the time required for approximately 50% (half) of a substance to decay,
to be consumed, to break down, or to be reduced.
For example, the half-life of Uranium-238 is 4.5 billion years,
of Carbon-14 is 5,730 years, of Cobalt-60 is 5.27 years, and of caffeine is 6 hours.
Percentages remaining: After 1 half-life, 50% remains; 2 half-lives, 25% remains;
3 half lives, 12.5% remains; and so on. After multiple half-lives, the amount of the substance becomes very, very, very small, but never truly reaches zero.
Base 1/2 is used when a specific
half-life is involved.
Half-Life:
A = A0 • (1/2)t/d
A = end result
A0= starting value
t = total time elapsed
* d = decay time for 50%
|
A half-life of x years would refer to
time that passed with 50% remaining.
Example:
You drink a cup of coffee that contains 250 mg of caffeine. If the half-life of caffeine is 6 hours, how long will it take until there are only 20 mg of caffeine left in your bloodstream?
Establish the formula:
A0 = 250 A = 20 (amount left)
d = 6 hours.
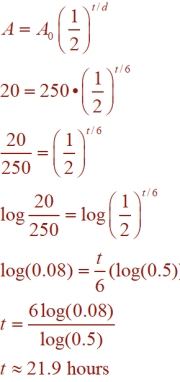
|
Base e is used with half-life as
it describes continuous decay.
Half-Life:
A = A0 • ekt
A = end result
A0= initial value
t = total time elapsed
k = decay constant (negative) |
Continuous decay occurs "all of the time",
not in "larger chunks" of time.
Example:
You drink a cup of coffee that contains 250 mg of caffeine. If the half-life of caffeine is 6 hours, how long will it take until there are only 20 mg of caffeine left in your bloodstream?
Establish the formula:
A0 = 250 A = 20 (amount left)
k = 6 hours
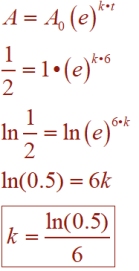
Find the k associated with
this half-life
situation called
the decay constant. |
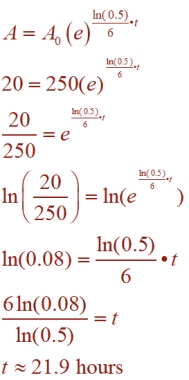
|
|
 (discrete decay: Solve using A = A0 • (1/2) t / d ) (discrete decay: Solve using A = A0 • (1/2) t / d )
The half-life of Iodine-125 is 59.4 days. How long, in days, will it take 40 grams to decay to 6.5 grams? Round to nearest tenth of a day.
A = 6.5, A0 = 40, d = 59.4 days
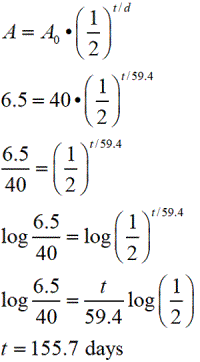 |
Substitute the known values.
Divide by 40 to isolate the term with the exponent.
Take the log of both sides.
Use the log properties to bring the exponent down to the base level.
Solve for t. |
|
 (chemicals continuous decay: A = A0ekt ) (chemicals continuous decay: A = A0ekt )
The half-life of Iodine-125 is 59.4 days. How long, in days, will it take 40 grams to decay to 6.5 grams? Round to nearest tenth of a day.
First, find k, the decay constant, so an equation for Iodine-125 can be formed.
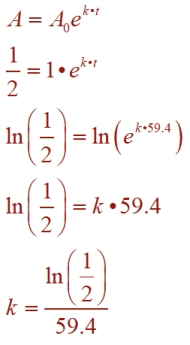 |
We are seeing a situation similar to what we saw with this formula and "doubling". The situation with half-life will always yield "half" of the starting amount. This allows us to fast forward on the values of
A and A0,
creating ½ and 1 respectively
You can see this formula at work in the computations on the left, solving for k. Using that solution, establish the formula, and
solve for the "time", t, on the right.
Write the equation using the result for k, starting value of 1, and the time = 96. Round to nearest tenth of a day. |
We now can write the equation for Iodine-125.
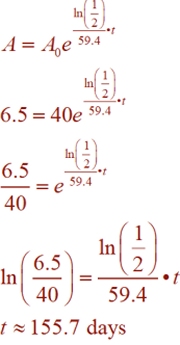 |
|

Things to keep in mind:
Sign of k:
•
If k is positive, you are dealing with growth.
• If k is negative, you are dealing with decay.
Doubling Time:
• The base value is 2 or e.
• For growth, the time needed to double the amount is 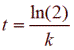 . .
Half-life:
• The base value is ½ or e.
• For decay, the time needed to get half the initial amount is 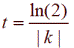 . .
Time is always positive.
|
This association among k, t, and ln(2) can be seen at work in solving for k
in the doubling example, and also in the decaying solutions:
 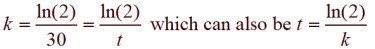

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|



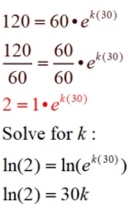
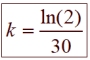
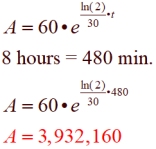
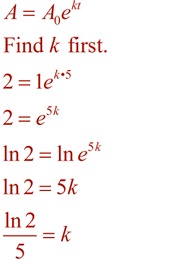
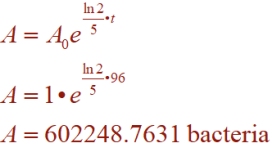
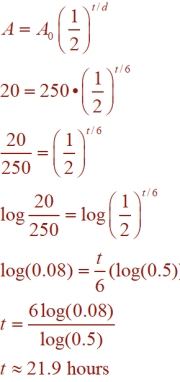
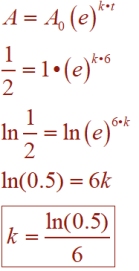
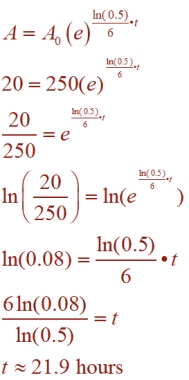
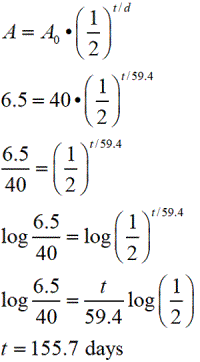
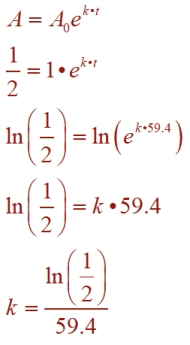
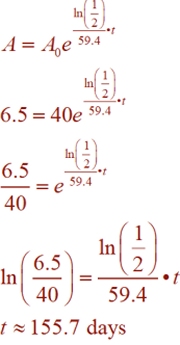
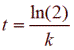 .
.