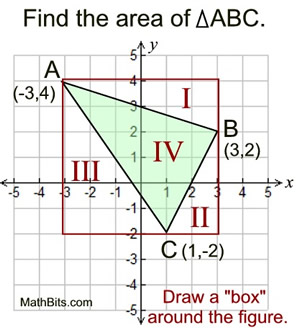
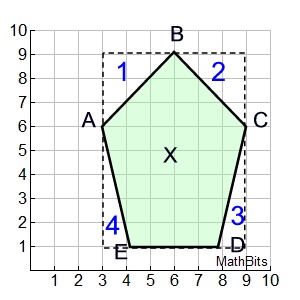
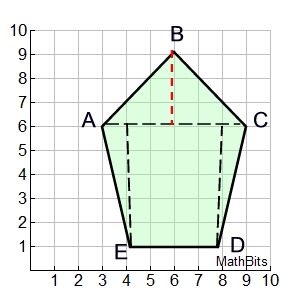
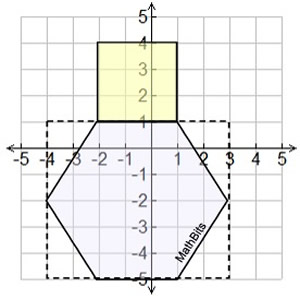
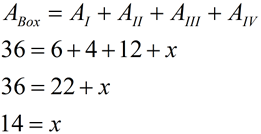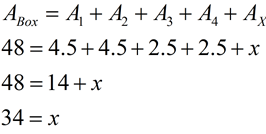This section will be "composing" polygons into rectangles as a strategy for finding the area of the polygon. We have already used this concept when we created a "box" around a figure graphed in the coordinate plane, so we could easily find its area.
Topical Outline | JrMath Outline | MathBitsNotebook.com | MathBits' Teacher Resources
|
|||||||||||||||||||||||||||||||||||