|
In geometry, formal definitions are formed using other defined words or terms. There are, however, three words in geometry that are not formally defined. These words are point, line and plane, and are referred to as the "three undefined terms of geometry".
While these words are "undefined" in the formal sense, we can still "describe" these words.
The descriptions, stated below, refer to these words in relation to geometry.
POINT
• a point indicates a location (or position) in space.
• a point has no dimension (actual size).
• a point has no length, no width, and no height (thickness).
• a point is usually named with a capital letter.
• in the coordinate plane, a point is named by an ordered pair, (x,y).
While we represent a point with a dot, the dot can be very tiny or very large. Remember, a point has no size. |
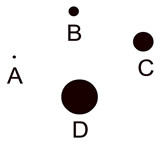 The size of the dot drawn to represent a point makes no difference. Points have no size. They simply represent a location.
The size of the dot drawn to represent a point makes no difference. Points have no size. They simply represent a location. |
LINE (straight line)
• a line has no thickness.
• a line's length extends in one dimension.
• a line goes on forever in both directions.
• a line has infinite length, zero width, and zero height.
• a line is assumed to be straight.
• a line is drawn with arrowheads on both ends.
• a line is named by a single lowercase script letter, or by any two (or more) points which lie on the line.
|
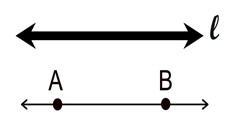
Lines can be labeled with a single script letter, or by two points on the line,  . The thickness of a line makes no difference. . The thickness of a line makes no difference. |
PLANE
• a plane has two dimensions.
• a plane forms a flat surface extending indefinitely in all directions.
• a plane has infinite length, infinite width and zero height (thickness).
• a plane is drawn as a four-sided figure resembling a tabletop or a parallelogram.
• a plane is named by a single letter (plane m) or by three coplanar, but non-collinear,* points (plane ABC).
|
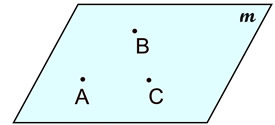 Plane m or Plane ABC
Plane m or Plane ABC.
While the diagram of a plane has edges, you must remember that the plane actually has no boundaries. |
* Collinear points are points that lie on the same straight line.
Coplanar points are points that line in the same plane.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|



