|
In our study of congruent triangles, it is important to understand under what conditions unique triangles can be drawn.
|
A "unique triangle" is a triangle for which there is no other triangle that has the same dimensions and shape. Duplicates of such triangles will all be congruent to one another. |
The word "unique" means "being the only one of its kind". |
|
 |
When attempting to draw a triangle, with given measurements, there can be three possible outcomes: |
| |
1. a unique triangle (one of a kind)
2. no triangle
3. more than one triangle (of different shapes and/or sizes) |
|
Let's see what combinations of measurements need to be given
to guarantee drawing a unique triangle.
Remember, you can flip, slide and rotate a unique triangle,
so it may look like different triangles, but, in reality, they are all the same triangle.
Measurements that guarantee drawing a unique triangle.
It is assumed in working with these measurement that the angles in the triangle will total 180º. |
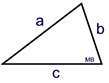
Given: 3 line segments, a, b, c
If the sum of the lengths of any two of the segments used as sides for the triangle is greater than the third segment, the triangle will be unique.
(Triangle Inequality Theorem at work.)
If this sum is not greater than the 3rd side, a triangle can not be drawn. |
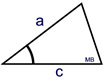
Given: 2 line segments (a, c) and the measure of the angle located between the segment sides
If two segments are used as sides with the measure of the angle between them given, the triangle formed will be unique.
The angle between the segments is referred to as the "included" angle. |
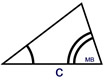
Given: measures of 2 ∠s and a segment (c) used between the angles
If two angles are used with the given segment as a side between them, the triangle formed will be unique.
The side between the angles, is referred to as the "include" side.
|
AAS (or SAA)
Angle-Angle-Side |
|
|
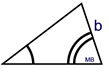
Given: measures of 2 ∠s and a segment (b) used NOT between the angles
If two angles are used with the given segment as a side, NOT between the angles, the triangle formed will be unique.
The segment formerly labeled as "a" could also have been used as the side NOT between the angles. |
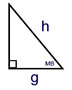
Given: a right triangle and
2 segments (g and h)
If the given segments are used for the hypotenuse and leg of a right triangle, the right triangle formed will be unique.
The "box" indicates an angle of 90º, and the hypotenuse is across from the box. |
The "included angle" in SAS is the angle formed by the two sides of the triangle being used.
The "included side" in ASA is the side between the angles being used. It is the side where the rays of the angles overlap.
The "non-included" side in AAS can be either of the two sides that are not directly between the two angles being used. |
|
Measurements that result in "NO" triangle or "many" triangles. |
If the sum of the angles in a triangle does not equal 180º, a triangle will not exist.
|
Triangle Inequality fails |
|
Not Unique
No Triangle |
The sum of the lengths of any two of the sides of the triangle must be greater than the third side to produce a triangle.
Triangle Inequality Theorem |
|
Not Unique
Many Triangles |
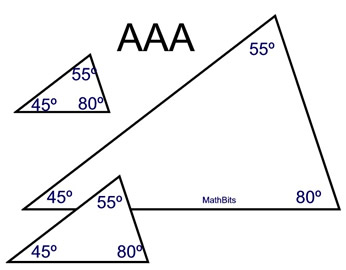
Given: the measures of 3 angles
(whose sum = 180º)
Using ONLY angle measurements, takes away the control over the lengths of the sides of the triangle, allowing for the side lengths to vary. Many different sized triangles can be drawn with these 3 angles. See diagram at the right.
These triangles are similar triangles. They are not unique and they are not congruent. |
 |
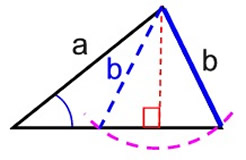
SSA or ASS
Side-Side-Angle |
|
Not Unique
Two Triangles |
Given: 2 segments (a, b) and the measure of an ∠ NOT between the sides
Since the angle is not between the sides, side b, as shown at the right, is free to "swing" into one of two different positions. Two different triangles can be formed.
|
We will see more of the "Donkey Theorem" in congruent triangles. HL is actually a special case of this situation which works ONLY in right triangles.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|