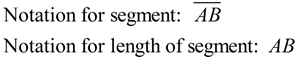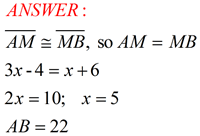|
A segment (or line segment) is a part of a line that is bounded by two distinct end points. It contains every point on the line between its end points.
|
|
Ruler Postulate: The points on a line can be paired (put into a one-to-one correspondence) with the real numbers. The distance between any two points is represented by the absolute value of the difference between the numbers. [Keep in mind that distances are always positive.]
|
The distance between D and F is | 0 - 2 | = 2.
The distance between C and E is | -2 - 1 | = 3.
The distance between A and C is | -3 - (-2) | = 1. |
On this diagram, you can "count" the units between the letters to determine the distance between the letters. |
Segment Addition Postulate
(Partition Postulate) |
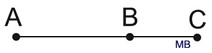
Statement: If B lies on the segment from A to C, then AB + BC = AC.
Also the converse: If AB + BC = AC, then B lies on the segment from A to C.
This is a "common sense" type of rule. If you draw a picture, this rule will be obviously true.
Remember that AB, BC, and AC refer to the lengths of the actual segments.
When you take a course in Geometry, you will see examples of this postulate referred to as the concept of "whole quantity", "the whole is equal to the sum of its parts" or "betweenness of points".
In this postulate, points A, B and C are collinear, meaning they all lie on the same line.
|
The midpoint of a segment is a point on the segment forming two segments of equal measurec (ongruent segments). |
|
Example:

|

|
|
|
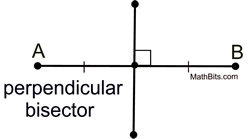
The bisector of a segment is a line, ray, or segment which cuts the given segment into two congruent segments.
|
|
The point where the bisector crosses the segment is the midpoint of the segment.
If the bisector is also perpendicular to the segment, it is referred to as the perpendicular bisector of the segment. |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|