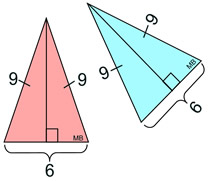
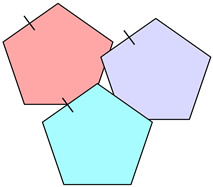
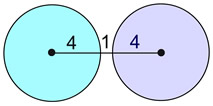
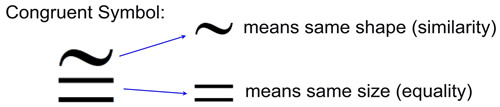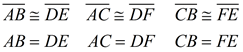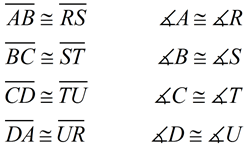As seen in the table above, even though two figures may be duplicates of one another (congruent), they may not appear in the same positions when first viewed. After a transformation, or series of transformations, however, one figure can be moved to coincide with the other.
Congruent geometric figures:
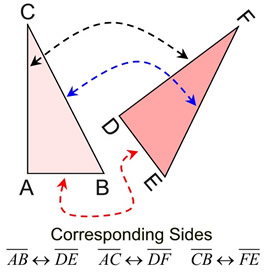
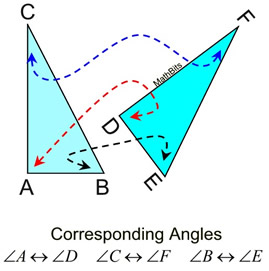
Parts that are in the same locations in identical figures are referred to as "corresponding" parts.
The corresponding angles of congruent figures are equal in measure.
The corresponding line segments of congruent figures are equal in length.
ΔABC is identical to ΔDEF
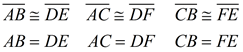
|
ΔABC is identical to ΔDEF
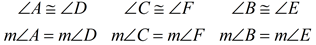 |
Matching Parts: When working with congruent geometric figures, locate the sides and the angles that "match up" (are in the same locations after a transformation). Sides and angles that "match up" are called corresponding sides and corresponding angles.
In congruent figures, the corresponding sides are congruent, and the corresponding angles are congruent. Notice the 8 facts known to be true about the two congruent trapezoids. |
Trapezoid ABCD  Trapezoid RSTU Trapezoid RSTU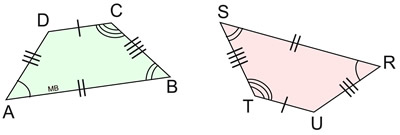
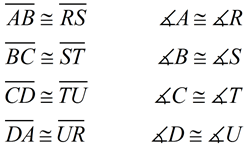 |
|
Marking Corresponding Parts:
Known information regarding the corresponding parts in congruent figures is often
marked on the diagrams. The corresponding congruent sides are marked with small straight line segments called
hash marks. The corresponding congruent angles are marked with
arcs.
The order of the letters in the names of the congruent figures displays the corresponding relationships. In this manner, even without the diagrams for our trapezoid example, you would know that ∠A would be congruent to ∠R, ∠B would be congruent to ∠S, and so on. In addition, 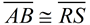 because these segments are in the same positions in each trapezoid's name.
because these segments are in the same positions in each trapezoid's name.
Thinking about "when" figures are congruent (identical):
1. Will figures be congruent if all of the corresponding sides and all of the corresponding angles are congruent? Most definitely! Having all corresponding sides and angles congruent is the essence of figures being identical (congruent).
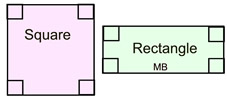
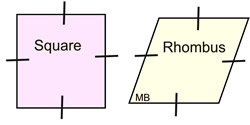
2. Will figures be congruent if all of the corresponding sides are congruent, but the corresponding angles are not congruent? The answer is "No"! Think about all of the possible situations and combinations that could occur. For example, the sides of a square and the sides of a rhombus could be congruent, but the angles of a rhombus need not be each 90º. |
 |
3. Will figures be congruent if all of the corresponding angles are congruent, but the corresponding sides are not congruent? The answer is "No"! Again, think about all of the possible situations. For example, the angles of a square and the angles of a rectangle are congruent, but the sides of the rectangle need not be the same length as the sides of the square. Or, there could also be the possibility that the second figure could be another square, but with different length sides. |
|