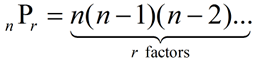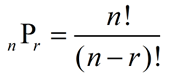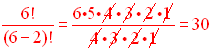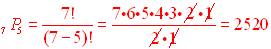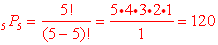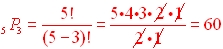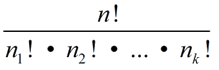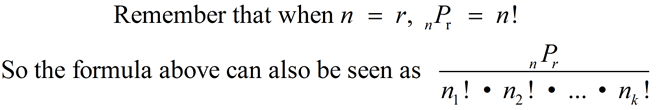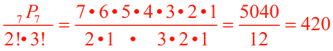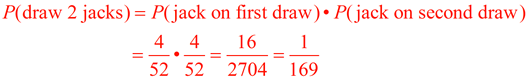|
A permutation is an arrangement of objects in specific order.
The order of the arrangement is important!! Order matters!!
 Permutations:
Permutations:
All possible ways of doing something! |
Consider, four dogs arranged in a line as shown. How many different ways could the dogs be arranged in this side-by-side pattern?
1,2,3,4
1,2,4,3
1,3,2,4
1,3,4,2
1,4,2,3
1,4,3,2
|
2,1,3,4
2,1,4,3
2,3,1,4
2,3,4,1
2,4,1,3
2,4,3,1 |
3,2,1,4
3,2,4,1
3,1,2,4
3,1,4,2
3,4,2,1
3,4,1,2 |
4,2,3,1
4,2,1,3
4,3,2,1
4,3,1,2
4,1,2,3
4,1,3,2 |
|
The number of different arrangements is 24 or 4! = 4 • 3 • 2 • 1.
There are 24 different arrangements, or permutations, of the four dogs sitting side-by-side.
The notation for a permutation:
n P r
n is the total number of objects
r is the number of objects chosen (wanted)
read: "n objects taken r at a time" |
|
For the dogs, there are"4 dogs taken 4 at a time".
4 P4 = 4 • 3 • 2 • 1 = 24 arrangements
|
|
|
For working
with
permutations
on your
calculator,
click here. |
|
|
Formulas for Permutations: |
Formula for a permutation:
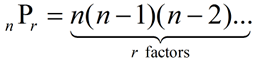
|
OR |
Formula for a permutation: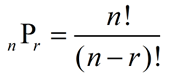 Remember that 0! = 1.
Remember that 0! = 1. |
 If n = r, as it did with the dogs, them nPr = n! for either formula. If n = r, as it did with the dogs, them nPr = n! for either formula. |

Examples:
1. Compute 6 P2
6• 5 = 30
(multiply two factors of the factorial starting with 6)
OR use formula:
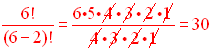
|
2. How many ways can 5 objects be arranged that are chosen from a set of 7 different objects.
7 P5 = 7 • 6 • 5 • 4 • 3 = 2520
(seven objects taken five at a time)
OR use formula:
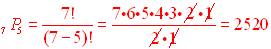
|
3. Find the total number of possible 5-letter arrangements of the letters s, c, o, r, e if each letter is used only once in the arrangement.
5 P5 = 5 • 4 • 3 • 2 • 1 = 60
OR use formula:
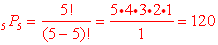 or simply 5! or simply 5!
|
4. How many different 3-digit integers can be made from the digits 5, 6, 7, 8, 9 if a digit can appear only once in a number.
5P3 = 5 • 4 • 3 = 60
OR use formula:
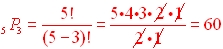 |

Dealing with "Special" Arrangements |
Consider the following example where special conditions are placed on the arrangement.
Task: Using the letters from the word "WIZARD", how many 6-letter arrangements, with no repetition, are possible, if:
a) the first letter must be a vowel
b) the first and last letters must be consonants
Solution:
a) Set up a visual of the six needed letters: ____ • ____ • ____ • ____ • ____ • ____
The first location must be a vowel (i, a), so there are only 2 ways to fill the first empty slot.
_2_ • ____ • ____ • ____ • ____ • ____
There are now 5 letters left to fill the remaining slots.
_2_ • _5__ • _4__ • _3__ • _2__ • _1__ = 240
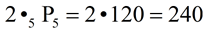
b) Again, visualize the 6 needed locations: ____ • ____ • ____ • ____ • ____ • ____
The first and last letters are consonants (w, z, r, d)
_4_ • ____ • ____ • ____ • ____ • _3__
The remaining locations are filled with the remaining 4 letters.
_4_ • _4__ • _3__ • _2__ • _1__ • _3__ = 288
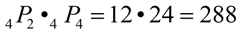

When dealing with permutations with repetition, remember that order still matters.
Task: How many 3 letter words can be made from the letters c, a, t, allowing for repetition of the letters?
Solution:
Set up a visual of the three needed letters: ____ • ____ • ____
There are 3 letters that can be used to fill the first slot. But, now, because repetition is allowed, we also have 3 letters to fill the second and third slots.
_3_ • _3__ • _3__ = 27 arrangements
|
27 arrangements with repetition: |
ccc
caa
ctt
cat
cta
cac
ctc
cca
cct |
aaa
acc
att
act
atc
aca
ata
aac
aat |
ttt
taa
tcc
tac
tca
tct
tat
ttc
tta |
|
|

 Dealing with repetition can become confusing when you encounter repetition of indistinguishable objects. Indistinguishable objects are simply items (such as letters) that are repeated in the original set. For example, if the word MOM was used instead of CAT, in the example above, the two M's are indistinguishable from one another, since they repeat. Using MOM, some of the answers would have been duplicates of one another because of the repeating M. Dealing with repetition can become confusing when you encounter repetition of indistinguishable objects. Indistinguishable objects are simply items (such as letters) that are repeated in the original set. For example, if the word MOM was used instead of CAT, in the example above, the two M's are indistinguishable from one another, since they repeat. Using MOM, some of the answers would have been duplicates of one another because of the repeating M.
When looking for answers that are not duplicates (unique answers), the problem of any letters or objects repeating in the original set must be addressed.
The number of different permutations of n objects, where there are n1 indistinguishable objects of style 1, n2 indistinguishable objects of style 2, ..., and nk indistinguishable objects of style k, is ;
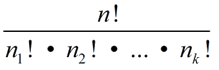 |
In general, repetitions are taken care of by dividing the permutation
by the factorial of the number of objects that are identical.

Examples:
1. How many different 6-letter words can be formed from the word SCHOOL ?

Divide by 2! because the letter O repeats twice.
|
2. How many different 7-digit integers can be written using all of the following 7 digits: 3,3,4,4,4,5,8 ?
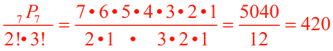
The 3 repeats twice and the 4 repeats three times, so divide by 2! • 3!
|

With Replacement; Without Replacement |
We have seen how "with replacement" and "without replacement" affect probability. These same situations appear when working with permutations.
Examples:
1. Two cards are drawn from a standard deck of 52 cards, without replacement.
What is the probability that both cards drawn are jacks?
There are 4 jacks in a deck of cards. The first card will NOT be returned to the deck before picking the second card.
 |
| 2. One card is drawn from a standard deck of 52 cards and then replaced into the deck. A second card is then drawn and replaced. What is the probability that a jack is drawn each time?
On the first draw, the probability of getting one of the four jacks in the deck is 4 out of 52 cards.
Because the jack is replaced into the deck, the probability of getting a jack on the second draw remains the same. Using the Counting Principle we have:
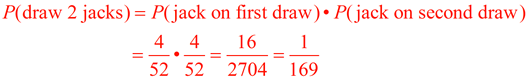
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|