|
In Geometry, "locus" is a "set of points" whose "location" satisfies a given condition (or rule). Think of "locus" as being a "path" or a "location" of points.
While the term "locus" (plural "loci") may sound confusing, it is really a simple idea. In geometry, locus is a way of looking at ideas and theorems we have already seen, and know to be true.
In two-dimensional geometry, a locus of points is a curve or a line. Locus is associated with an equation. While there is not a specific formula to find a locus, there will be steps to follow to determine the location of the locus. |
 |
If you plot the points, one at a time, that satisfy the rule for a locus, you will see a "path" where these points will lie (depicted by a dashed line). If you consider an infinite number of the points, you will see the curve or the line representing the locus path.
Due to their connections to equal distances, parallel lines, and angle bisectors, questions pertaining to these locus theorems may also contain a construction component. While these theorems may sound confusing at first reading, their concepts should seem familiar.

There are six locus theorems (rules) that are popular in geometry.
|
These six "new" locus theorems are actually alternate statements about geometric concepts that we already know. A discussion of locus may also utilize constructions to determine where specific points are located. Let's take a look at the concept connections, and the associated constructions.
| Locus Theorem 1: The locus at a fixed distance, d, from point P is a circle with the given point P as its center and d as its radius. |
Definition of Circle (from JrMath): A circle is the set of points equidistant from a given point called the center.
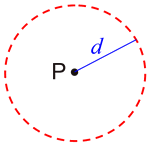
"a fixed distance" = "equidistant"
"from point P" = "from a given point" |
|
|
Construction:
|
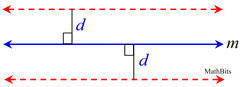
| Locus Theorem 2: The locus at a fixed distance, d, from a line m, is a pair of parallel lines at a distance of d from line m, and located on either side of m. |
Concept on Parallel Lines (from Geometry): Parallel lines are always the same distance apart, which is referred to as being "equidistant".
"a fixed distance" = "equidistant"
"parallel lines" = "parallel lines" |
Lines are assumed to be straight lines. Therefore, the locus will be two straight lines. Distance is measured as the perpendicular distance between the given line and the locus line.
It could also be measured between the two locus lines. |
Construction: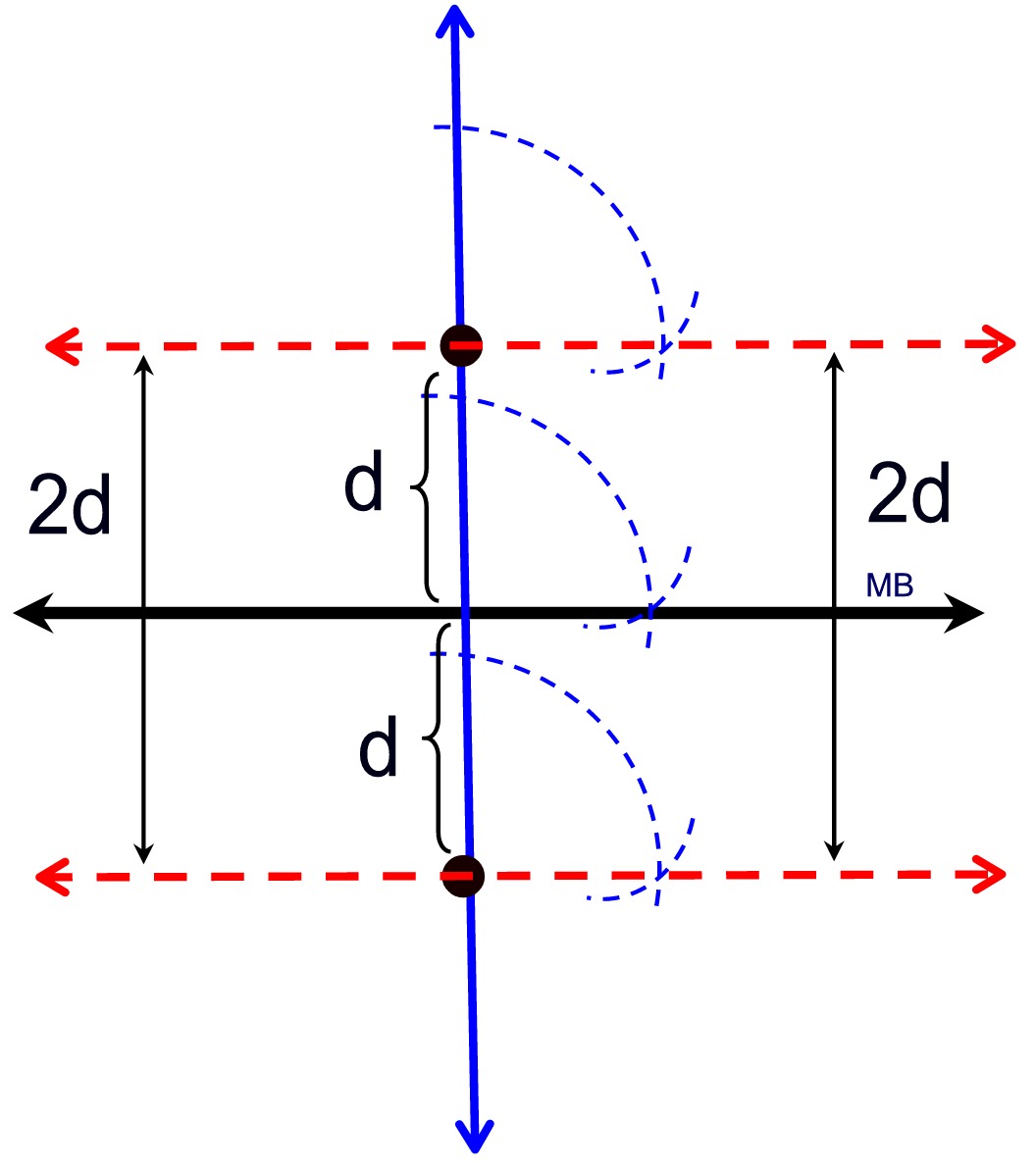 |
| Locus Theorem 3: The locus equidistant from two points A and B, is the perpendicular bisector of the line segment joining the two points.
(Sound familiar?) |
Theorem (from Geometry): The perpendicular bisector of a line segment is the set of all points that are equidistant from its endpoints.
"equidistant 2 pts." = "equidistant endpoints"
"line segment" = "line segment" |
|
|
Construction:
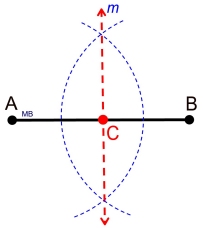
|
| Locus Theorem 4: The locus equidistant from two parallel lines, m1 and m2, is a line parallel to both m1 and m2 and halfway between them.
|
Concept on Parallel Lines (from Geometry): Parallel lines are always the same distance apart, which is referred to as being "equidistant".
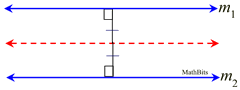
"equidistant 2 lines." = "the same distance"
"parallel lines" = "parallel lines" |
|
Parallel lines are straight lines. A point is located halfway between the two lines with distance measured as the perpendicular distance The path will be another parallel line halfway between the lines as parallels are everywhere equidistant. |
Construction: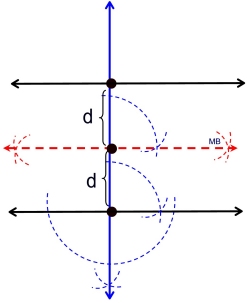 |
| Locus Theorem 5: The locus in the interior of an angle equidistant from the sides of the angle is the bisector of the angle (exclusive of the vertex).
(Sound familiar?) |
Concept on Angle Bisector (from Geometry): If a point lies anywhere on an angle bisector, that point is equidistant from the two sides (rays) of the bisected angle.
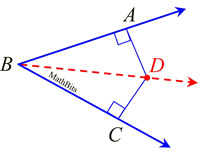
"in the interior" = "lies anywhere on"
"equidistant" = "equidistant" |
|
|
Construction:
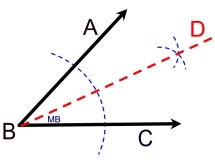
|
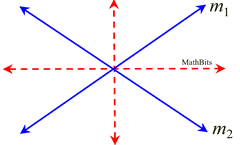
| Locus Theorem 6: The locus equidistant from two intersecting lines, m1 and m2, is the pair of lines which bisect the angles formed by the lines m1 and m2. |
Extended Application of Concept on Angle Bisector (from Geometry): If a point lies anywhere on an angle bisector, that point is equidistant from the two sides (rays) of the bisected angle.
|
Construction:
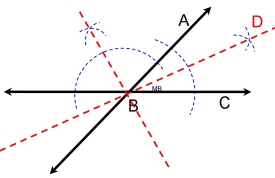
|
All conic sections (circles, ellipses, parabolas, and hyperbolas) are defined using the term "locus", the location of a set of points.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|