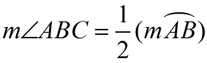We have seen "inscribed angles" whose vertices lie on the circle, and whose rays (sides) must intersect two points on the circle (the sides must be chords).
In this lesson, we will examine another angle whose vertex is also on the circle,
but whose rays (sides) do NOT meet the definition of an inscribed angle.
The sides of these angles are not BOTH chords.
|
A tangent-chord angle of a circle is an angle formed by a tangent and a chord drawn to the point of tangency on the circle. (The vertex lies on the circle.) |
|
Notice that this angle is named by reference to its rays (sides).
Thus, its name gives a clear picture of what the angle looks like.
Tangent-Chord Angle (theorem)
The measure of a tangent-chord angle
equals ½ the measure of its intercepted arc.
Tangent Chord Angle = 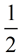 Intercepted Arc Intercepted Arc
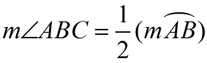 |
In the diagram at the right, ∠ABC is a tangent-chord angle with an intercepted minor arc from A to B.
|
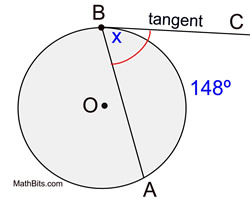
m∠ABC = 74º |
|
|
NOTE: Yes, if we extended the tangent line to the left of point B, we would form another tangent-chord (obtuse) angle which would measure ½ the
"major" intercepted arc..
Whether you are to deal with the minor arc or major arc
will be indicated in the diagram or wording.
For example, the labeling may be a single letter, "x", an arc, or lettering of the desired angle, "∠ABC".
 |
We have now seen that there are two types of angles,
inscribed angles AND tangent-chord angles,
that have their vertices ON the circle
and measure ½ the intercepted arc.
|
So, roughly speaking, if the vertex of an angle is on the circle, the formula is ½ the intercepted arc.