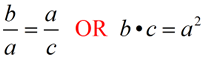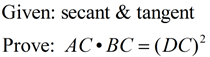|
This lesson deals with "segments" in varying positions in relation to circles.
These "segments" may be chords, other portions of secants, and/or portions of tangents.
The formulas for the lengths of these segments will be investigated.

|
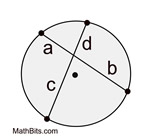
If two chords intersect in a circle, the product of the lengths of the segments of one chord equal the product of the segments of the other. |
| |
|
Intersecting Chords Formula:
(segment piece) x (segment piece) =
(segment piece) x (segment piece) |
Formula: a • b = c • d
|
|
Example:
|
Solution:
• As the formula states:
a • b = c • d
4 • 6 = 8 • x
24 = 8x
x = 3
|
|
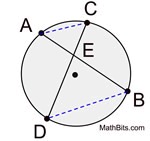
PROOF:
|
Proof:
|
|

|
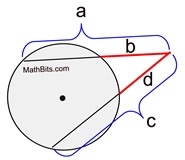
If two secant segments are drawn to a circle from the same external point, the product of the length of one secant segment and its external part is equal to the product of the length of the other secant segment and its external part. |
| |
|
Secant-Secant Formula:
(whole secant) x (external part) =
(whole secant) x (external part) |
Formula: a • b = c • d
|
|
Example:
Given circle O with two secants, as marked,
intersecting at A. Find x. |
Solution:
• As the formula states:
(whole) • (external) = (whole) • (external)
12 • 20 = (x+10) • 10
240 = 10x + 100
140 = 10x
14 = x
|
|
PROOF:
|
Proof:
|
|

|
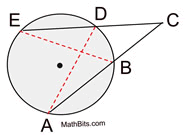
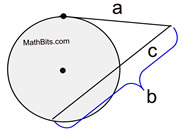
If a secant segment and tangent segment are drawn to a circle from the same external point, the length of the tangent segment is the geometric mean between the length of the secant segment and the length of the external part of the secant segment. |
Alternate Wording: |
... the product of the length of the secant segment and its external part equals the square of the length of the tangent segment. |
| |
|
Secant-Tangent Formula:
 OR OR
(whole secant) x (external part) = (tangent)2 |
Formula: 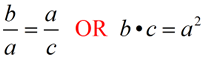 |
|
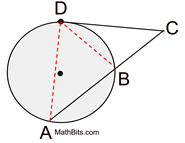
Example:
Given circle O with a secant and a tangent,
as marked, intersecting at A. Find x. |
Solution:
• Using formula: 
 x • (x+12)= 82
x • (x+12)= 82
x2 + 12x = 64
x2 + 12x - 64 = 0
(x + 16)(x - 4) = 0
x = 4
reject negative answer since x is a measurement
|
|
PROOF:
|
Proof:

|
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|