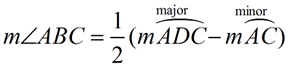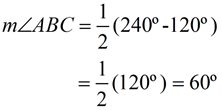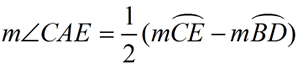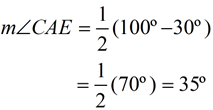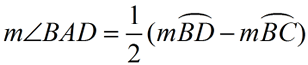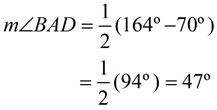Angles Formed Outside Circle - Two Tangents, Two Secants, Tangent Secant

Angles formed Outside the Circle
"Two Tangents", "Two Secants", "Tangent Secant"MathBitsNotebook.com

Topical Outline | Geometry Outline | MathBits' Teacher Resources

Terms of Use Contact Person: Donna Roberts

This lesson is divided into three sections,
all dealing with angles formed by intersections outside of the circle.

Section 1: Angle formed by two tangents
Section 2: Angles formed by two secants
Section 3: Angle formed by a tangent and a secant

	The formulas for all THREE of these situations are the same:
Angle Formed Outside = 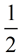(DIFFERENCE of Intercepted Arcs)

These differences always yield a positive result. (larger arc subtract smaller arc)

SECTION 1: Two Tangents:

An angle formed by two tangents is an angle created when two tangent lines to the circle intersect at a point outside of the circle.

Angle formed by Two Tangents:

∠ABC is formed by two tangents intersecting outside of circle O. The intercepted arcs are arc minor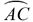

and major arc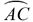

. These two arcs together comprise the entire circle.

Angle Formed by Two Tangents
=

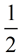(DIFFERENCE of Intercepted Arcs)

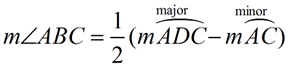
(When subtracting, start with the larger arc.)

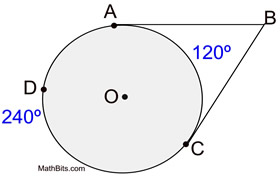
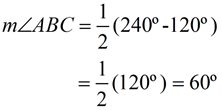m∠ABC = 60º

Note: When dealing with two tangents, you are dealing with the ENTIRE circle (360º). This will not be the case in the next two sections.

Note:

It can be proven that:
∠ABC and central angle ∠AOC are supplementary (add up 180º).

Also, the angle formed by the two tangents and the first minor intercepted are also supplementary
(add to 180º).

This supplementary association will NOT apply to Two Secants, nor to Tangent-Secant diagrams.

Example 1:

Given two tangents, find x.

Solution:
• Since the major arc is 230º. the minor arc is
360 - 230 = 130º.

• The angle x will be half the difference of the two intercepted arcs.

• x = ½ (230 - 130) = ½ (100) = 50º

Example 2:

Given two tangents, with m∠C = 65º.
Find the number of degrees in the minor arc from point A to point B.

Solution:
• If you remember the "note" from above, you remember that ∠C and its minor arc are supplementary. (180 - 65 = 115)
Thus the minor arc has a measure of 115º.

• If you forget the "note", you can still solve this problem algebraically with the formula.
Let minor arc = x. and let major arc = 360 - x.
Apply the formula: 65 = ½ (360-x - x)
65 = ½ (360 - 2x)
130 = 360 - 2x
2x = 230
x = 115º

PROOF: Angle formed by Two Tangents

• Note that the Exterior Angle Theorem was used in this proof.

SECTION 2: Two Secants:

An angle formed by two secants is an angle created when two secant lines through a circle intersect at a point outside of the circle.

Angle formed by Two Secants:

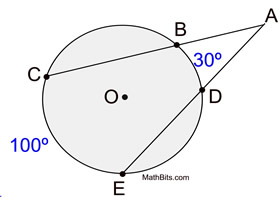
∠CAE is formed by two secants intersecting outside of circle O at point A. The intercepted arcs are arc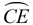

and arc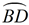

Angle Formed by Two Secants
=

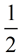(DIFFERENCE of Intercepted Arcs)

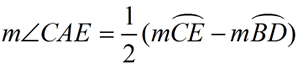
(When subtracting, start with the larger arc.)

While the tangent-tangent angle utilized the entire circle, the secant-secant angle will only use the portions of the circle that fall between the secant lines.

ang2sec
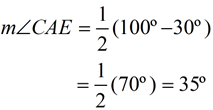
angleSecm2
m∠CAE = 35º

Example 1:

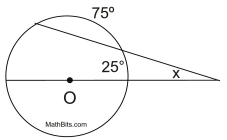
Given two secants, with one secant passing through the center of the circle.
Find x.

Solution:
• Since one secant is passing through the center, we are dealing with a semicircle (180º).
On the top half of the circle, we have
25º + 75º + ? = 180º. The missing top arc is 80º.

• Apply the formula: x = ½ (80 - 25)

• x = ½ (55) = 27½º

Example 2:

Given two secants, find x.

Solution:
• Apply the formula: 2x = ½ (7x + 15 - 45)

• Solve for x:
2x = ½ (7x + 15 - 45)
2x = ½ (7x - 30)
4x = 7x - 30
30 = 3x
10 = x

PROOF: Angle formed by Two Secants

• Note the similarity to the previous proof.
Again, the Exterior Angle Theorem was used in this proof.

SECTION 3: Tangent-Secant:

An angle formed by one tangent and one secant is an angle created when a secant lines passes through a circle intersects outside the circle with a line tangent to the circle.

Angle formed by a Tangent and a Secant:

∠BAD is formed by a tangent and a secant intersecting outside of circle O. The intercepted arcs are arc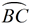

and arc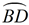

Angle Formed by Tangent and Secant
=

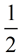(DIFFERENCE of Intercepted Arcs)

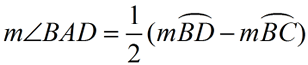
(When subtracting, start with the larger arc.)

Like the secant-secant angle, the tangent-secant angle utilizes only portions of the circle that fall between the secant and tangent lines.

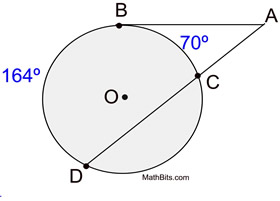
ang2sec
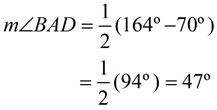
angSTm2
m∠BAD = 47º

Example 1:

Given a secant and a tangent.
Find x.

Solution:
• We are missing an arc needed for the formula.
Since the circle totals 360º, we can find the missing arc: 360 - (235 + 45) = missing arc.
Missing arc = 80º

• Apply the formula: x = ½ (80 - 45)

• x = ½ (80 - 45)
x = ½ (35)
x = 17½º

Example 2:

Given a secant and a tangent.
Find x.

Solution:
• Apply the formula: 45 = ½(165 - x)
Be sure to subtract the smaller arc from the larger arc.

• Solve for x:
45 = ½(165 - x)
90 = 165 - x
x = 75º

PROOF: Angle formed by one Secant and one Tangent:

• Again, note the similarity in the three proofs from this lesson.
They all follow the same pattern, with adjustments for the diagrams.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use".

Topical Outline | Geometry Outline | MathBitsNotebook.com | MathBits' Teacher Resources
Terms of Use Contact Person: Donna Roberts