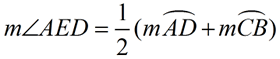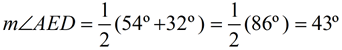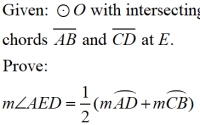Starting with this lesson, and the following lessons, we will be investigating angles,
related to circles, whose measures involves the use of two arcs of the circles.
|
An intersecting chords angle of a circle is an angle formed by two chords (or secants) intersecting in the interior of the circle.
(If the point of intersection is the center of the circle, central angles are formed.) |
|
The two chords intersecting inside the circle form four angles.
At the point of intersection are two sets of congruent vertical angles,
formed in the corners of an X that is created by the chords.
Intersecting Chords Angle (theorem) |
The measure of an angle formed by two chords intersecting inside a circle, is one-half the sum of the measures of the arcs intercepted by the angle and its vertical angle.
Angle Formed by Two Chords
= 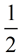 (SUM of Intercepted Arcs) (SUM of Intercepted Arcs)
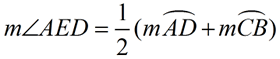 |
In the diagram at the right, ∠AED is an angle formed by two intersecting chords in the circle. Notice that the intercepted arcs belong to the set of vertical angles.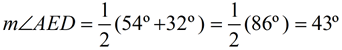 also, m∠BEC = 43º (vertical angle)
also, m∠BEC = 43º (vertical angle)
m∠CEA and m∠BED = 137º by straight angle formed.
|
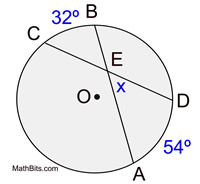 m∠AED = 43º
m∠AED = 43º
Once you have found ONE of these angles, you automatically know the sizes of the other three by using vertical angles (which are congruent) and adjacent angles forming a straight line (whose measures add to 180º). |
|
|
|

Example 1:
|
Solution:
• This is a situation of having to find the angle formed by two intersecting chords.
• Formula needed: the angle = ½ the sum of the intercepted arcs
x = ½(42 + 105)
x = ½(147)
x = 73½º *
|
|
| Example 2:
|
Solution:
• This is a situation of two intersecting chords forming an angle of 99º.
• Formula needed: the angle = ½ the sum of the intercepted arcs (and work in reverse).
99 = ½(114 + x) [multiply by 2 to remove ½]
198 = 114 + x
x = 84º *
|
|

PROOF of Intersecting Chords Angle Theorem:
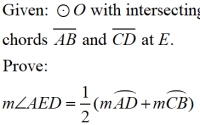
For ease of reading,
let m∠1 = m∠AED
|
|
|