|
The notations used in geometry can be a bit confusing at first.
Basically, there are notations that refer to the actual geometric figures, and there are notations that refer to the measures (sizes, lengths) of the figures.
|
 |
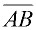 is a segment.
The bar over the letters means you is a segment.
The bar over the letters means you
are referring to the segment itself
(the actual physical segment). |
|
AB is a length, a number.
The letters, without a bar on top, refer to the length of the segment
from point A to point B. |
|
|
|

By definition, the term congruent means "having equal length or measure".
Figures are congruent (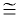 ).
Segments are congruent. Angles are congruent. Triangles are congruent. The congruent symbol is used when referring to the actual physical entities (diagrams). ).
Segments are congruent. Angles are congruent. Triangles are congruent. The congruent symbol is used when referring to the actual physical entities (diagrams).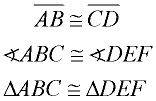 |
|
Numerical values are equal. (=)
When referring to a length or measure, the equal sign should be used. You speak of numbers as being equal (or not equal).
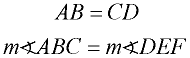
(Triangles are not referred to as being "equal",
since they are not numbers, and we do not speak of the measure of a Δ.) |
|
Let's look at the notation needed when we want to say that the lengths of the sections of this segment equal the length of the entire segment.
 |
Given 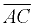 .
We can observe from the diagram that AB = 3 and BC = 8.
Consequently, AC = 11. (The whole is equal to the sum of its parts.)
|
Write: AB + BC = AC. Do NOT write: 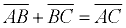 You add the segment lengths. You cannot "add" the actual segment diagrams.
You add the segment lengths. You cannot "add" the actual segment diagrams. |
While most textbooks follow this notation process,
you may find some sources that show varying notations.
This web site will be following the notations as described on this page.
|

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|