This page will only be working with "simple" rational equations which
contain numerical denominators or denominators with simple monomial variables.
|
A rational equation is an equation that contains one, or more, rational expressions. Remember: equations have equal signs. |
|
Rational Expression
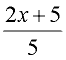 NO equal sign!
NO equal sign! |
Rational Equation
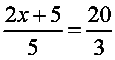 Equal sign!
Equal sign! |
|
In an equation, unlike in an expression, it is possible to multiply both sides of the equation by the same value and maintain a true equation. Multiplying both sides by a common denominator maintains a balanced equation,
and gets rid of those pesky denominators.
If the equation contains addition or subtraction, be careful to multiply each term (distribute) on both sides of the equal sign.
|

 Solving the simplest type of Rational Equations: Solving the simplest type of Rational Equations:
1. Perhaps the easiest type of rational equation to solve is the one that is expressed as a proportion (one fraction equal to another fraction). We simply treat the problem as a proportion and solve by cross product ("cross multiply"). Remember, that in a proportion, the product of the means equals the product of the extremes. |
1. Solve this equation for x:
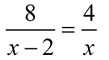 |
2. Cross multiply: |
|
3. Distribute and solve for x. |
3. 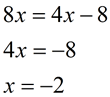 |
4. Check in original equation. |
4. Check:
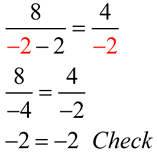 |

Now, the real work begins!
 To Solve Rational Equations: To Solve Rational Equations:
• Identify the least common denominator (LCD).
• Multiply each side of the equation by the LCD.
• Simplify (the denominators should be gone).
• Solve the resulting equation.
• Check the answers for possible extraneous roots.
|
 Solving Rational Equations with Numerical Denominators: Solving Rational Equations with Numerical Denominators:
1. Find the least common denominator.
In this example, the least common denominator (LCD) is 6.
|
1. Given: 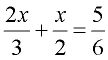 solve for x. LCD = 6 |
2. Multiply both sides of the equation by the least common denominator. Note the parentheses on the left. You need to distribute across the parentheses.
Hint: You need to multiply each term by the common denominator.
|
2. 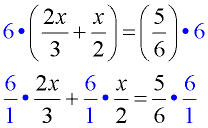 |
3. Reduce and simplify each term. |
3. 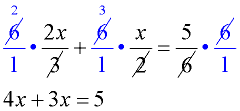 |
4. Solve for x. |
4.
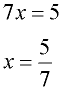
|
5. Check in original equation. |
5. Check:
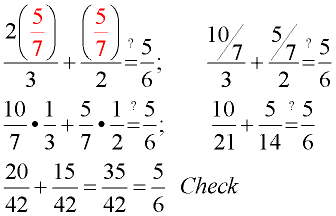 |

 Solving Rational Equations with Variable Denominators: Solving Rational Equations with Variable Denominators:
 Solving rational equations with variables in the denominators involves manipulating and rewriting the terms. These "new forms" of the original equation may produce solutions that "do not work in the original equation". These answers are called extraneous solutions, and are not real answers at all. Always check your answer(s) in the original equation to be sure you do not have an extraneous solution.
Extraneous solutions will be a common occurrence in Algebra 2. Solving rational equations with variables in the denominators involves manipulating and rewriting the terms. These "new forms" of the original equation may produce solutions that "do not work in the original equation". These answers are called extraneous solutions, and are not real answers at all. Always check your answer(s) in the original equation to be sure you do not have an extraneous solution.
Extraneous solutions will be a common occurrence in Algebra 2. |
1. Determine domain values that will create zero denominators.
|
1. Given: 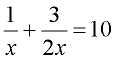 solve for x. solve for x.
Domain: x ≠ 0 |
2. Find the least common denominator.
In this example, the least common denominator (LCD) is 2x.
Multiply both sides of the equation by the least common denominator. Note the parentheses on the left. You need to distribute across the parentheses. |
2. 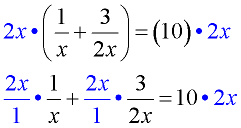 |
3. Reduce and simplify each term. |
3. 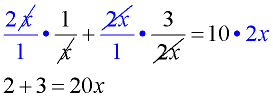 |
4. Solve for x. |
4. 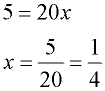 |
5. Check to be sure the answer is not a value that caused a zero denominator in the original equation. |
5. The answer is not x = 0, which causes zero denominators in the original equation, so our answer is a valid solution.
Check:
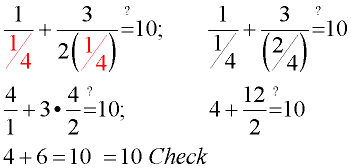 |

 Examples: Examples:
Example 1: (Numerical denominators)
Solve:
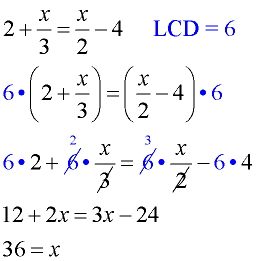
Check:
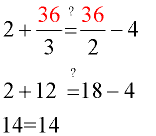 |
Example 2: (Variable denominators)
Solve: (Domain: x ≠ 0)
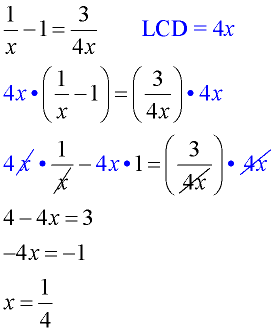 Check:
Check:
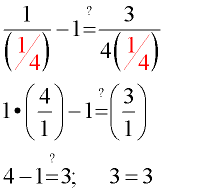 |
Example 3: Method 1: (proportion)
Solve:
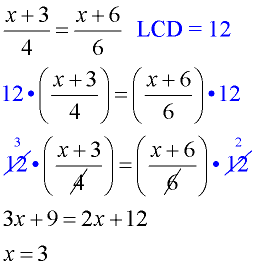
Check:
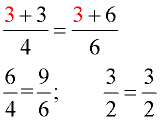
|
Example 3: Method 2: (proportion)
Since Example 3 is a proportion, it can be solved by using "cross multiply". (In a proportion, the product of the means equals the product of the extremes.)
Solve:
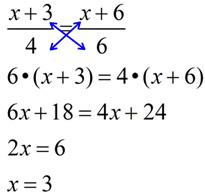
Check: Same as Method 1
|
Example 4: (extraneous solution)
Solve:
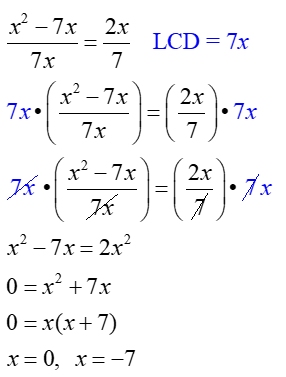 |
The solution x = 0 causes a problem, since the check is showing division by zero.
We also know that the value of x = 0 caused a zero denominator in the original equation.
x = 0 is an extraneous solution.
The solution x = -7 is the only solution for this problem.
(This problem could also have been solved using cross multiplication.) |
Check:
 |

|
How to use your graphing calculator with
rational equations
Click here. |
|
|
|
How to use
your graphing calculator with
rational equations,
Click here. |
|
|
|