Transformations on Exponentials
 

We know that transformations have the ability to move functions by sliding, reflecting, rotating, stretching, and shrinking them. Let's see how these changes will affect the exponential function:

Exponential Function ( y = abx ) Transformation Examples:
Translation y = b(x - h) + k
horizontal by h: vertical by k:

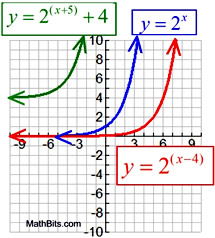
Tgraph4
Domain: x ∈ Real numbers
Range: if a > 0, y > k
(if a < 0, range y < k )

Translations:

Vertical Shift: f (x) + k

Horizontal Shift: f (x + h)


Reflections:

-f (x) over x-axis

f (-x) over y-axis
Reflection
y = a(bx)
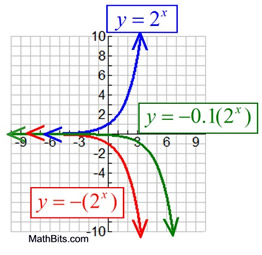
Domain: x ∈ Real numbers
For these examples, if a > 0, y > 0,
if a < 0, y < 0.

Vertical Stretch/Compress
y = cbx
Stretch (|c| > 1):
Compress or Shrink
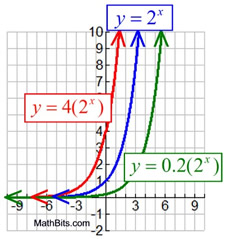
(0 < |c| < 1): Tgraph2
Domain: x ∈ Real numbers
Range: y > 0

Vertical Stretch/Compress

c • f (x) stretch (c > 1)

c • f (x) compress (0 < c < 1)

 

Horizontal Stretch/Compress

f (c • x) stretch (0 < c < 1)

f (c • x) compress (c > 1)

 Horizontal Stretch/Compress y = bcx
Stretch (0 < |c| < 1):
Compress or Shrink
( |c| > 1):


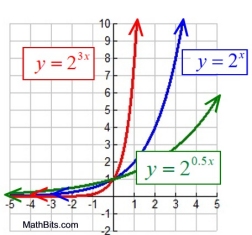
Domain: x ∈ Real numbers
Range: y > 0

All 4 transformations combined:    y = a • bc(x - h) + k
Note: The independent variable is x with the domain of real numbers.


divider

NOTE: The re-posting of materials (in part or whole) from this site to the Internet is copyright violation
 and is not considered "fair use" for educators. Please read the "Terms of Use".