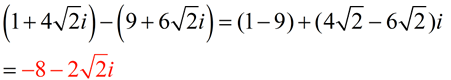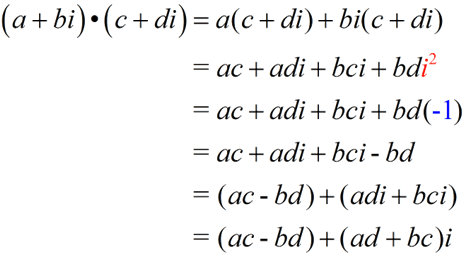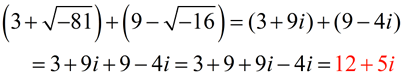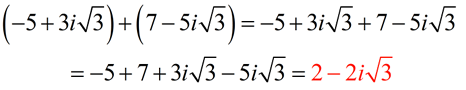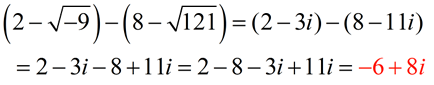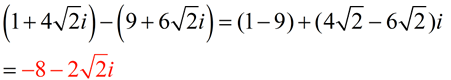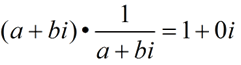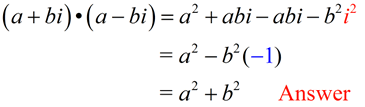Add and Subtract Complex Numbers |
When performing the arithmetic operations of adding or subtracting on complex numbers, remember to combine "similar" terms. Also check to see if the answer must be expressed in simplest a+ bi form.
| Addition Rule: (a + bi) + (c + di) = (a + c) + (b + d)i |
Add the "real" portions, and add the "imaginary" portions of the complex numbers.
Notice the distributive property at work when adding the imaginary portions:
bi + di becomes (b + d)i .
| Additive Identity: (a + bi) + (0 + 0i) = a + bi |
| Additive Inverse: (a + bi) + (-a - bi) = (0 +0i) |
 ADD: (6 + 4i) + (8 - 2i)
ADD: (6 + 4i) + (8 - 2i)
Express answer in a + bi form.
Adding parts: (6 + 4i) + ( 8 - 2i) = 6 + 4i + 8 - 2i = 6 + 8 + 4i - 2i = 14 + 2i
Addition Rule grouping: (6 + 4i) + ( 8 - 2i) = (6 + 8) + (4 - 2)i = 14 + 2i
 ADD: 3 + (-2 - 4i) + (5 + i) + (0 - 2i)
ADD: 3 + (-2 - 4i) + (5 + i) + (0 - 2i)
Express answer in a + bi form.
3 + (-2 - 4i) + (5 + i) + (0 - 2i) = 3 - 2 - 4i + 5 + i - 2i = 6 - 5i
It is not necessary to always show the "grouping" of terms unless you are asked to do so.
Just be careful of the signs when subtraction is involved.
 ADD:
ADD: 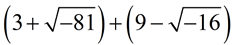
Express answer in a + bi form.
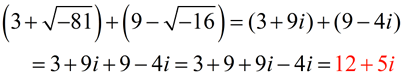
Notice that the radicals were simplified before the addition began.
 ADD:
ADD: 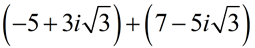
Express answer in a + bi form.
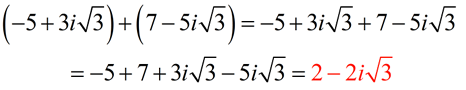
| Subtraction Rule: (a + bi) - (c + di) = (a - c) + (b - d)i |
Subtract the "real" portions, and subtract the "imaginary" portions of the complex numbers.
Notice the distributive property at work when subtracting the imaginary portions:
bi - di becomes (b - d)i .
 SUBTRACT: (10 + 3i) - (7 - 4i)
SUBTRACT: (10 + 3i) - (7 - 4i)
Express answer in a + bi form.
(10 + 3i) - (7 - 4i) = 10 + 3i - 7 - (-4i) = 10 - 7 + 3i + 4i = 3 + 7i
Subtract Rule grouping: (10 + 3i) - (7 - 4i) = (10 - 7) + (3 - (-4))i = 3 + 7i
 SUBTRACT:
SUBTRACT: 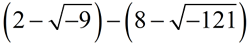
Express answer in a + bi form.
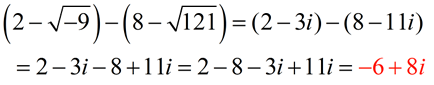
 SUBTRACT:
SUBTRACT: 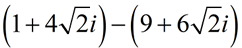
Express answer in a + bi form.