|
The rigid transformations maintain congruence.
(reflection, translation, rotation = flip, slide, turn) |
We saw a brief mention of the connection between transformations and congruent figures in the Geometry section under the discussion of congruent figures. Let's take a closer look at this relationship now that we are more comfortable with transformations.
We now know that the rigid transformations (reflections, translations and rotations) preserve the size and shape of the figures. That is, the pre-image and the image are always congruent.
The table below should now make more sense. If two figures are congruent, it is possible to use one, or more, rigid transformations to establish that the congruency is actually true. Starting with one of the figures, is there a rigid transformation, or a series of rigid transformations, that could lead to the other figure? If yes, the figures will be congruent, because rigid transformations preserve size and shape.
The figures in this chart are congruent.
It is possible to find one, or more, rigid transformations between the two figures.
It is possible to turn, flip and/or slide one figure so it will fit exactly on the other figure.
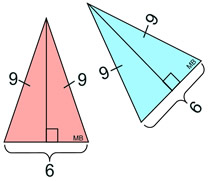
Two congruent isosceles triangles. The blue triangle is a "turn" (rotation) of the red triangle.
 |
Two congruent cartoon birds. The bird on the right is a "flip" (reflection) and "slide" (translation) of the bird on the left. |
Three congruent regular pentagons. The purple and blue pentagons are "slides" of the red pentagon.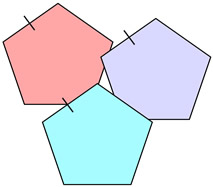 |
Two congruent designs. The design on the right is a "turn" (rotation) of the design on the left. |
Two congruent circles. The circle on the right is a "slide" (translation) of the circle on the left.
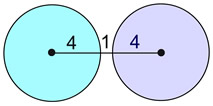 |
Two congruent shapes. The shape on the right is a "slide" (translation) of the shape on the left.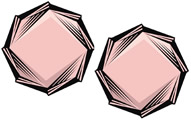 |
The concept of congruent triangles can be stated as:
"When triangles are congruent, one triangle can be moved
(through one, or more, rigid transformations) to coincide with the other triangle."
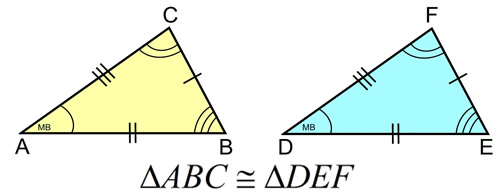
Triangle DEF is a horizontal translation of triangle ABC.
(or vice versa)
Example in the Coordinate Plane:
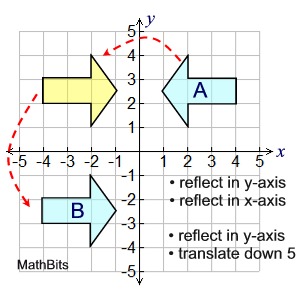
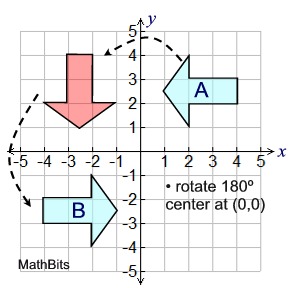
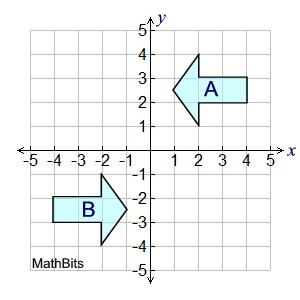
EXAMPLE: Arrow A and arrow B are congruent. Find one or more rigid transformations that will verify that these arrows are congruent.
Assume arrow A to be the pre-image and arrow B to be the image.
|
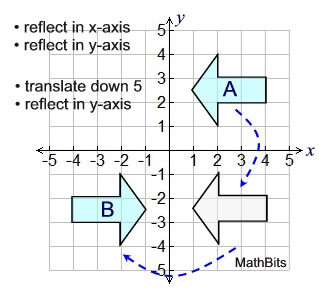
Solution: It is possible in questions of this type that more than one answer may exist.
Five possible solutions are shown below.
Four of the solutions use two rigid transformations, and one uses one.
 |
|
|