|
When two or more transformations are combined to form a new transformation, the result is called a sequence (or a composition) of transformations. In a sequence of transformations, the first transformation produces an image upon which the second transformation is then performed.
 |
EXAMPLE:
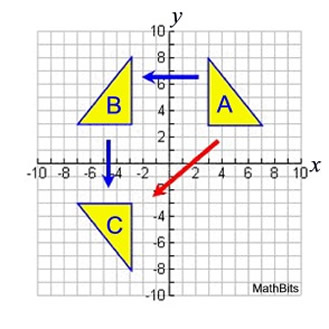
In the graph at the left, triangle A is reflected over the y-axis to get image triangle B. Then image triangle B is reflected over the x-axis to get image triangle C. Under this sequence of transformations, triangle C is the final image of triangle A.
It is possible that a sequence of two transformations may be renamed by only one other transformational method. For example, the sequence of a line reflection in the y-axis followed by a line reflection in the x-axis, from this example, could be described as a single transformation of a reflection in the origin.
This is NOT necessarily the case in all sequences of transformations.
|
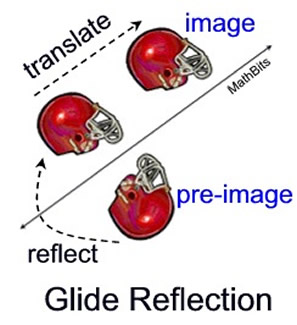
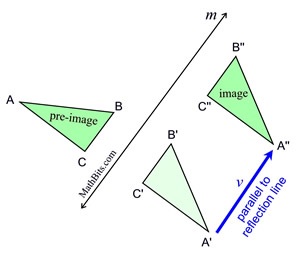
A popular sequence of transformations in which a specific pattern of a reflection followed by translation occurs is called a glide reflection. There will be a reflection of a figure, followed by a translation (a "glide" or slide) of the figure along the line of reflection.
 A glide reflection is the composition of a reflection and a translation, where the translation is parallel to the line of reflection, m. A glide reflection is the composition of a reflection and a translation, where the translation is parallel to the line of reflection, m. |
A glide reflection is commutative. Reversing the direction of the composition will not affect the outcome. It does not matter whether you glide first and then reflect, or reflect first and then glide. |
 |
|
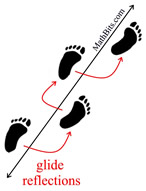
Footprints are an example of several glide reflections. In the diagram at the left, you are seeing the original "step" on the left foot, followed by the "step" on the right foot, which is the "result" of the glide reflection.
When compared to the diagram of the triangles, shown above, you are not seeing ΔA'B'C' (reflection) in the footprints. You are only seeing the final image ΔA''B''C''.
|
Properties preserved (invariant) under
a glide reflection:
(Since these properties are preserved under both the reflection and the translation, they are preserved under the glide reflection.)
1. distance is preserved (lengths of segments are the same)
2. angle measures (remain the same)
3. parallelism (parallel lines remain parallel)
4. collinearity (points stay on the same lines)
5. midpoint (midpoints remain the same in each figure)
-----------------------------------------------------
6. orientation NOT preserved (lettering order does not remain the same)
|
|
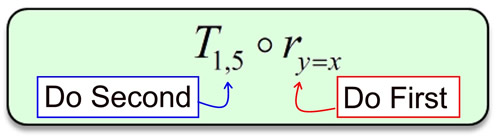
 There is a notation for working with sequences of transformations,
There is a notation for working with sequences of transformations,
but we will not be using this notation at this level.

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|