|
|
Integers: ... -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ... |
(no fractions or decimals) |
Prime numbers are integers (greater than 1) that can be divided exactly by only 1 or by itself.
It has exactly two factors.
|
Prime Numbers:
2, 3, 5, 7, 11, 13, 17,
19, 23, 29, 31, 37, 41, 43, 47, 53, 59. 61, 67, 71, 73, 79, 83, 89, 97, ...
Positive integers that are not
prime numbers
are called composite numbers.
All whole numbers are either prime or composite, except for 0 and 1, which are neither.
A composite number is a
positive integer
that
has
more
factors than just 1 and itself.
A composite number has a finite number of factors.
Examples of composite numbers are:
4, 6, 8, 9 10, 12, 14, 15, 16, 18, 20, 21, ...
The number 24 is an example of a composite number.
Its factors are 1, 2, 3, 4, 6, 8, 12, and 24.
All of these factors divide exactly into 24.
|
|
|
Factors are numbers you multiply to get another number. |
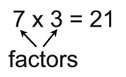 |
Prime factorization is the process of finding only prime numbers that will multiply together to form a starting number.
It breaks a number down into its prime factors. |
This process of prime factorization is based upon the Fundamental Theorem of Arithmetic:
|
Fundamental Theorem of Arithmetic
|
Any integer greater than 1 is either a prime number, or can be written as a unique product of prime numbers. (The order of the prime numbers is ignored.) |
This basically means that every integer
greater than one, that is not prime, can be written as the multiplication (the product) of
only prime numbers.
And there is only one such set of primes per number.
|
 |
Examples: While you can start your factoring with any prime number that will divide exactly into your number, starting with the smaller prime numbers is usually the easiest process. The diagrams shown below with the segments, are called factor trees.
Prime factorization can be used to reduce fractions.
(This process will always get you the simplest form of the fraction.)
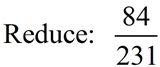 |
Solution using prime factorization:
|
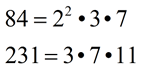 |
|
|

• A number is called a perfect number if it is equal to the sum of its positive divisors excluding itself.
Consider 6: its factors are 1, 2, 3 and 6
1 + 2 + 3 = 6 making 6 a perfect number.
Consider 28: its factors are 1, 2, 4, 7, 14, 28
1 + 2 + 4 + 7 + 14 = 28 making 28 a perfect number. |
 |

NOTE: The re-posting of materials (in part or whole) from this site to the Internet
is copyright violation
and is not considered "fair use" for educators. Please read the "Terms of Use". |
|
|