The sieve of Eratosthenes (276 BC - 194 BC) is an ancient method for finding all prime numbers up to a specific given value.
The concept is to progress through a chart of consecutive integers removing the multiples of each prime number, starting with the first prime number 2.
How it Works:
Start with a chart of consecutive positive integers.
Multiples of the prime numbers will be crossed out throughout the chart. This chart will be from 1 to 100.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
41 |
42 |
43 |
44 |
45 |
46 |
47 |
48 |
49 |
50 |
51 |
52 |
53 |
54 |
55 |
56 |
57 |
58 |
59 |
60 |
61 |
62 |
63 |
64 |
65 |
66 |
67 |
68 |
69 |
70 |
71 |
72 |
73 |
74 |
75 |
76 |
77 |
78 |
79 |
80 |
81 |
82 |
83 |
84 |
85 |
86 |
87 |
88 |
89 |
90 |
91 |
92 |
93 |
94 |
95 |
96 |
97 |
98 |
99 |
100 |
1. |
Cross out 1 (it is not a prime). |
2. |
Start with 2. Circle 2 as a prime number, but cross out all multiples of 2 (every even number). |
3. |
Now, move to the next prime 3. Circle 3 as a prime number, but cross out any multiple of 3 remaining in the chart. |
4. |
Now, move to 5. Circle 5 as a prime number, but cross out any multiple of 5 remaining in the chart. |
5. |
Now, move to 7. Circle 7 as a prime number, but cross out any multiple of 7 remaining in the chart. |
6. |
Continue this process for each prime number you encounter on the chart. Remember that a prime is divisible only by 1 and itself. |
7. |
The circled values in the chart are the prime numbers between 1 and 100. |
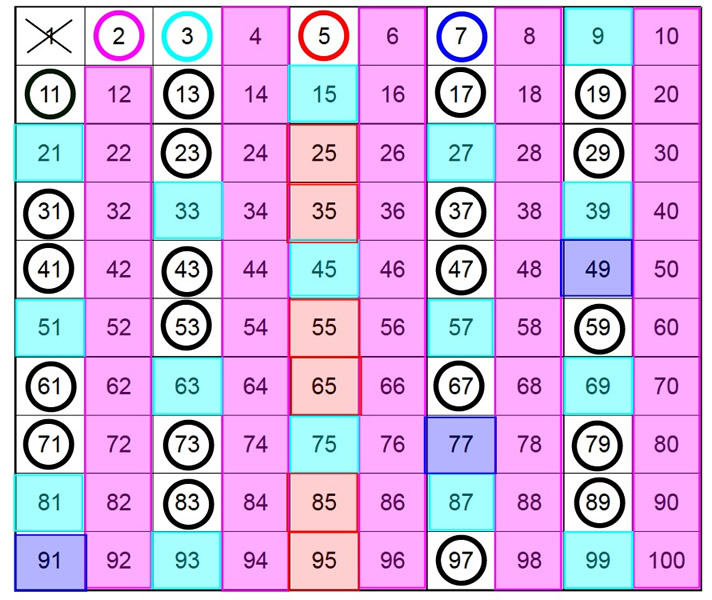
The multiples of the values circled in black had already been colored,
or do not exist in this small chart.
The prime numbers between 1 and 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97
|