You have already worked with inequality statements.
Let's refresh those skills and toss in a few new items and terms.
 |
The purpose of inequalities is to compare two values (or expressions). |
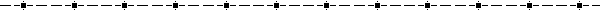
| Notations for Inequalities: |
| Inequality Notations: |
a > b ; a is strictly greater than b |
a 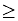 b ; a is greater than or equal to b |
a < b ; a is strictly less than b |
a 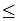 b ; a is less than or equal to b |
a ≠ b ; a is not equal to b |
Hint: The "open" (wider spread) part of the inequality symbol always faces the larger quantity. |
Notations without the "or equal to" portion of the symbol (such as just > or just < )
are referred to as Strictly Increasing, or Strictly Decreasing.
The term "strictly" does not allow for "equal to".
The expressions with equality included ( < or > ) are referred to as just Increasing or Decreasing.
Forms of notation include:
1. Inequality Symbol: x > -2
2.
Text: x is greater than negative two
3. Set-Builder Notation: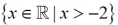 
4. Interval Notation: (-2, ∞)
|
Displayed on Number Line:
|
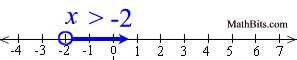
(see more about forms of notations at Notations for Solutions)
| Basic Properties of Inequalities: |
(properties apply to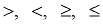 
)
If a > b, then a + c > b + c. |
Addition Property of Inequality |
If a > b, then a - c > b - c. |
Subtraction Property of Inequality |
If a > b and c > 0, then ac > bc. |
Multiplication Property of Inequality
|
Notice that c > 0.
If c < 0, reverse the direction of the final inequality. |
If a > b and c > 0, then  . |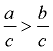
Division Property of Inequality |
| If a < b and b < c, then a < c. |
Transitive Property of Inequality |
| If a > b then b < a. |
Sometimes called the "Reversal Property". (Converse) |
We saw in the Real Number Chart a property called the Law of Trichotomy.
This Law of Trichotomy describes the only three relationships
that can exist between two values. ("tri" measn three).
a > b, a = b, a < b
In essence, this law states that every real number is either positive, negative or zero.
(Consider b = 0 to see why this statement is true: a > 0, a = 0, a < 0.)
| Verify Rule for Solving Inequalities: |
|
 Remember: |
The process of solving a linear inequality is the same as solving a linear equation, except ...
... when you multiply (or divide) an inequality by a negative value,
you must change the direction of the inequality. |
Let's first get an intuitive idea of what is happening
and why this "exception" is actually needed.
We know that 3 is less than 7.
Now, lets
multiply both sides by -1.
Examine the results (the products). |
... written 3 < 7.
... written (-1)(3) ? (-1)(7)
... written -3 ? -7
|
On a number line, -3 is to the right of -7, making -3 greater than -7.
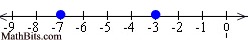-3 > -7
We have to reverse the direction of the inequality,
when we multiply by a negative value, in order to maintain a "true" statement. |
Now, let's look at a more algebraic justification
as to why this "exception" is actually needed.
Statement: If you multiply (or divide) both sides of an inequality by a negative value,
you will need to change the direction of the inequality.
1. If a > b, then -a < -b. |
1. Translation of statement (mult. by -1). |
2. a > b |
2. Start with the "given" a > b. |
3. a - b > b - b |
3. Subtract b from both sides. |
4. a - b > 0 |
4. Additive Inverse Property b - b = 0 |
5. a - a - b > 0 - a |
5. Subtract a from both sides. |
6. 0 - b > -a |
6. Additive Inverse, Additive Identity |
7. -b > -a |
7. Additive Identity Property |
8. -a < -b |
8. Read in reverse (converse) |
